Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 [ 49 ] 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

2.7.2. Решение обратных задач с помощью генетических алгоритмов

Решение обратной задачи по определению параметров Q0, т, T1 на

интервале обучения сводится к поиску минимума невязки (2.78), т. е. к задаче нелинейного программирования.

Эффективный поиск оптимальных значений Q0 , т , T1 может быть

организован с помощью генетических алгоритмов (ГА) [37, 38].

В основе ГА лежит постепенное приближение к оптимальному решению, реализуемое путем создания «популяции» возможных решений и организации «эволюции» этих решений путем их попарного «скрещивания» и «воспроизводства» потомства (новых возможных решений) со случайными «мутациями». Каждая особь (возможное решение) оценивается мерой ее «приспособленности» согласно тому, насколько оно удовлетворяет критерию качества данной оптимизационной задачи. Воспроизводить «потомство» имеют возможность только наиболее «приспособленные» решения. Менее приспособленные особи «воспроизводят» потомков с меньшей вероятностью, так что те свойства, которыми они обладают, будут постепенно исчезать из популяции в процессе эволюции.

Скрещивание наиболее приспособленных особей приводит к тому, что исследуются наиболее перспективные участки пространства поиска. В конечном счете, популяция будет сходиться к оптимальному решению задачи.

Наличие наследственности является преимуществом ГА по сравнению с совершенно случайными методами поиска решений (например, методом Монте-Карло), когда на новом шаге поиска никак не используется информация о результатах предыдущих проб.

Скорость определения минимума невязки I1 повышается при ограничении области поиска оптимальных значений параметров Q0 , т , T1 .

Заметное сужение области поиска может обеспечить условие

T1 - 0.43т- t*<At*, полученное с учетом равенства (2.77). Здесь t* - момент времени, при котором относительная скорость отбора р, определенная по данным истории разработки месторождения, принимает максимальное значение, At* - погрешность оценки t*.

Исходя из потенциала добывающих скважин, можно также получить достаточно надежную интервальную оценку максимальной добычи

Q0< Q0 < .

Оценка величины T1 может быть получена путем аппроксимации гиперболой начального участка кривой роста накопленной добычи нефти.

Для крупных месторождений Западной Сибири (500 и более скважин) был проведен анализ точности прогноза модели (2.74) и широко распространенных характеристик вытеснения (моделей С. Н. Назарова-Н. В. Сипачева, А. М. Пирвердяна и других).

Среднеквадратичное отклонение на интервале экзамена от фактических данных приведено на рис. 2.13.

Среднеквадратичное отклонение, %

14 12 10 8

Модели:

-О- Н.В. Сипачева -А.М. Пирвердяна

-□- С.Н. Назарова, Н.В. Сипачева -О- С.Н. Капице!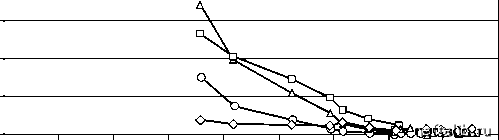

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

Обводненность, доли единицы

Рис. 2.13. Зависимость среднеквадратичного отклонения прогноза добычи нефти

от обводненности на интервале обучения

Легко заметить, что среднеквадратичное отклонение прогноза добычи нефти по модели (2.74) даже при малых значениях обводненности (порядка 45% на правом конце интервала обучения) приводит к приемлемым результатам. Таким образом, эту модель можно использовать уже на ранних стадиях разработки крупных месторождений для обоснованного прогноза добычи нефти.

2.8. О методах идентификации модели упругого пласта

Математическое моделирование процессов нестационарной фильтрации осложняется отсутствием надежных априорных оценок сжимаемости коллекторов и насыщающих их флюидов. Реальные значения коэффициента эффективной сжимаемости пласта могут довольно сильно отличаться от обычно принимаемых значений (~ 510-4 МПа-1). Поэтому сжимаемость пластовых систем целесообразно определять опытным путем, на основе решения обратной задачи идентификации модели упругого пласта

по промысловым данным о закачке и отборе жидкостей, а также о динамике пластового давления. В настоящем разделе рассматриваются некоторые общие подходы к этой проблеме и обсуждаются конкретные алгоритмы расчетов.

Решение поставленной задачи весьма чувствительно (в связи с малой сжимаемостью пород и флюидов) относительно точности определения разности объемов закачанной воды и отобранной жидкости. Одним из источников погрешностей служит то, что расход воды измеряется со значительно меньшей точностью, чем добыча нефти. В случае многопластовых систем данные по отбору нефти также ненадежны, поскольку разделение продукции по пластам производится приближенно, часто чисто расчетным путем.

Следует также учесть, что на поддержание пластового давления расходуется не весь зарегистрированный объем закачанной воды, поскольку возможны утечки воды через литологические окна, связывающие разные пласты, а также потери воды из-за негерметичности поверхностных водоводов и обсадных колонн нагнетательных скважин. Иногда могут наблюдаться и обратные перетоки из соседних пластов. Дополнительные сложности могут быть связаны с вторжением в продуктивный пласт законтурной воды.

При формализованном описании утечки и вторжение воды могут быть учтены введением в уравнение материального баланса некоторых дополнительных членов и поправочных коэффициентов. Поскольку априорная информация о проявлении подобных процессов зачастую отсутствует, то задача идентификации математической модели упругого пласта должна быть поставлена в широком смысле: требуется определить не только параметры (коэффициенты) модели, но и саму структуру модели. Последнее необходимо потому, что вид модели косвенным образом учитывает проявление тех или иных процессов, влияющих на баланс жидкостей.

Как уже отмечалось в разделе 2.3, при обработке экспериментальных данных качество решения задач идентификации существенно зависит от сложности моделей. Излишнее усложнение модели приводит, как правило, к повышенной неустойчивости решения обратной задачи, поэтому ниже основное внимание уделяется проблеме выбора оптимальной сложности модели упругого пласта.

Простейшее уравнение материального баланса можно записать в виде

= Qs -Qh -Qe, (2.80)

Plt=t = P0,

где b = , в и - коэффициент эффективной сжимаемости и поро-вый объем пласта, P - среднее пластовое давление, Qs, QH, Qe - объемы