
 |
|
|
Главная Переработка нефти и газа
Таким образом, в условиях неопределенности игровые подходы оказываются более соответствующими содержанию задач, чем методы, основанные на «разыгрывании» случайных состояний природы методом Монте-Карло. Применение последнего требует знания вероятностей распределения неизвестных параметров, а эта информация, зачастую, отсутствует. Рассмотренные выше критерии принятия решений могут быть использованы при анализе ситуаций самого различного масштаба: от дизайна ГТМ на отдельных скважинах до составления проектов разработки крупных месторождений. Следует подчеркнуть, что эти методы дают намного больше, чем обычный анализ чувствительности решений относительно изменения исходных данных. Если анализ чувствительности позволяет просто оценить пределы изменения выигрыша, то игровые методы предлагают одновременно и формальные алгоритмы выбора решений. 5.7. Системный анализ нроцессов разработки нефтяных месторождений Как уже неоднократно отмечалось, системы любой природы, независимо от природы составляющих элементов и отношений между ними, подчиняются некоторым общим закономерностям [39], знание которых облегчает принятие решений в условиях неопределенности. В частности, важную информацию, необходимую для управления, предоставляют исследования универсальных сценариев развития природных систем, количественных закономерностей чередования эволюционных и критических (переходных) периодов. В основе многих динамических процессов лежит экспоненциальный закон, в соответствии с которым скорость изменения характеристики x пропорциональна ее текущему значению где k - константа роста. kx (t), (5.66) соизмерима с годовыми расходами некоторых крупных компаний на научно-исследовательские работы. Несмотря на некоторую условность подобных расчетов, приведенные цифры позволяют оценить, по крайней мере, порядок потерь, связанных с недостатком информации. Таблица 5.5 Упущенная выгода при М=22500 кг (в млн. долларов) т 1,29 0,9 0,9 = 1,43. На плоскости т- и процесс развития по описанной схеме можно изобразить в виде ступенчатой линии, представленной на рис. 5.30. В основном, этот сценарий развития соответствует представлениям Шмальгаузена, который считал, что процессы роста начинаются экспоненциальной фазой, которая в дальнейшем переходит в степенной закон, характеризующийся убыванием константы скорости роста [42]. Для систем, развитие которых происходит при более или менее постоянных внутренних и внешних условиях, экспоненциальная зависимость описывает весь процесс развития. Однако при постепенном изменении этих условий могут быть достигнуты критические значения параметров, при которых экспоненциальное развитие теряет устойчивость и в системе появляются колебания («флаги катастроф» [40]), присущие процессам кризисного типа. В такие моменты начинают функционировать адаптационные механизмы, формирующие новые режимы экспоненциальной эволюции с иными значениями темпа роста. В работе [41] неустойчивости такого типа предлагается анализировать с помощью динамического уравнения с запаздывающим аргументом = kx(( -т), (5.67) где т - характерное время запаздывания. Поскольку с ростом системы ее инерционность возрастает, время запаздывания т считается возрастающей функцией времени. Для процессов, описываемых моделью (5.67), существуют экспоненциальные режимы развития x = x0eu, которые являются стабильными при выполнении условия [41] ит< 1,29. (5.68) При постепенном увеличении времени запаздывания наступает критический момент, когда неравенство (5.68) перестает выполняться. Экспоненциальная эволюция с темпом развития и становится неустойчивой, и включаются процессы самоорганизации, приводящие к уменьшению темпа роста. При этом вновь начинает выполняться неравенство (5.68), что обеспечивает стабильный рост до тех пор, пока увеличение т не приведет к новым кризисным явлениям. В [41] показано, что в период перестройки темп роста и уменьшается (при 10%-м «запасе прочности») до значения и =-. Таким образом, величина скачка в темпах роста, которая должна иметь место при достижении временем запаздывания критического уровня, будет составлять величину 1,29 Уменьшение темпов роста можно учесть в явном виде, если перейти к модели с константой роста, зависящей от времени. Аппроксимируя функцию k(t )гиперболической зависимостью, получим = ka x(t). dt ta Решение этого уравнения с начальным условием t 10 (5.69) (5.70) имеет вид при 0 <a< 1 (e = 1 -a< 1, k1 ln x = k1te + ln c, x = x0exp[1(te - t(f ) k0 (5.71) при a = 1. 1 -a , c - постоянная интегрирования) ln x = k0ln t + ln c x = x0 (5.72) U2 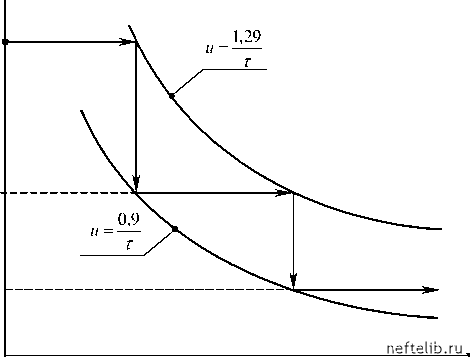 Рис. 5.30. Эволюция сложных систем 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 [ 115 ] 116 117 118 119 120 121 |
||||||||||||||
 |
 |