Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 [ 118 ] 119 120 121

5.8. Синергетика принятия решений

Информация, относительно которой нужно принять решение, практически никогда не бывает полной. Пользуясь математической терминологией, можно было бы сказать, что проблема принятия решения некорректно поставлена. В этом разделе мы, следуя книге Г. Хакена [46], кратко расскажем о том, как процессы принятия решений могут быть описаны на языке синергетики.

Как человек восполняет недостаток информации? В основном, путем использования сходства между данной ситуацией и аналогичными ситуациями, с которыми он встречался в прошлом (то есть методом аналогий, об этом мы уже говорили ранее). Показательны в этом смысле случаи, когда люди оказываются на грани жизни и смерти. Многие свидетельствуют, что в такие мгновения человек вспоминает (в обратной последовательности) всю свою жизнь. Таким образом, мозг лихорадочно ищет в жизненном опыте схожие моменты, чтобы в считанные секунды найти единственно верное решение. Помогает ему в этом то, что, согласно исследованиям профессора Я. Мияситы, человек никогда ничего не забывает. Вся воспринятая им информация хранится в височных долях серого вещества мозга, и обычные проблемы с памятью - это всего лишь трудности «считывания» информации.

В работах Г. Хакена с сотрудниками показано, что процесс поиска аналогов при принятии решений можно описать нелинейными уравнениями, схожими с известными каноническими уравнениями синергетики, характеризующимися множеством особых точек и сложной динамикой.

Известным механическим аналогом, используемым при наглядном представлении нелинейной динамики, является движение шарика по криволинейной поверхности. Используя этот подход, мы можем идентифицировать принятые решения найденные аналоги с дном долин, а процесс поиска решений - с нахождением шарика на склоне холма (см. рис. 5.34). Интересную ситуацию моделируют на этом рисунке точки C и D - два близлежащих минимума. Если шарик подвержен влиянию малых спонтанных возмущений, то он будет бесконечно долго колебаться между C и D . Эти осцилляции между двумя или более решениями («муки выбора») всем знакомы и увековечены в парадоксе «Буриданов осел». Подобные осцил-

Возвращаясь к рассмотренному выше месторождению Магнус, отметим, что, как показывают расчеты, на участке сбалансированного заводнения энтропия принимает наименьшее значение.

Вообще, энтропия оказывается весьма полезным инструментом динамического анализа процессов разработки и находит все большее применение в мониторинге нефтяных и газовых месторождений [44].

ляции между двумя решениями возникают и при разглядывании неоднозначных картин. Так, на известной картине мы сначала видим портрет Эйнштейна, а потом - трех купающихся девушек, потом опять портрет Эйнштейна и т. д. Все видели и другие подобные изображения - куб Нек-кера или картины «Юная красавица или дряхлая старуха?», «Ваза или два профиля?» (см. рис. 5.35) и др.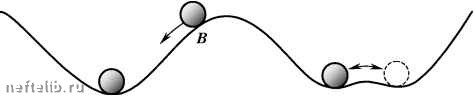

Рис. 5.34. Механическая модель динамики принятия решения A - принятие решения; B - поиск решения; C и D - осцилляции между двумя решениями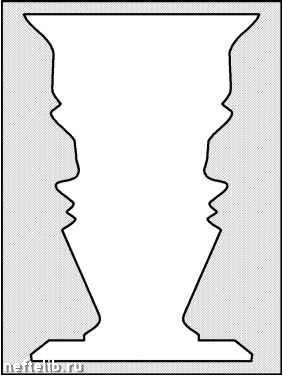

Рис. 5.35. Ваза или два профиля?

В общих чертах процесс узнавания аналогов можно описать следующим образом [46]. В памяти человека хранится информация о множестве различных жизненных ситуаций и оптимальных алгоритмов действия в этих ситуациях (информационные паттерны). После того как жизнь «предъявила» человеку новую ситуацию, в его мозге начинается конку-

рентная борьба между паттернами, в результате которой побеждает один из паттернов, наиболее близкий к анализируемой действительности. Здесь уместно вновь привести аналогию с лазером (см. раздел 1.3), в котором волна одной частоты побеждает все остальные. Самое общее представление о математических моделях, описывающих динамику распознавания, можно дать на следующем примере.

В задаче об определении оптимальной длины трещины ГРП (см. раздел 5.6) неопределенным является распределение вероятностей P j различных значений проницаемости kj (j = 1,2,к,n). Расчеты показывают, что

решение этой задачи существенно зависит от того, к какому из следующих четырех видов (паттернов) относится реальное распределение:

1) вероятности pj растут с ростом kj;

2) вероятности pj уменьшаются с ростом kj;

3) вероятности Pj имеют экстремум внутри интервала изменения k;

4) вероятности pj не зависят от проницаемости (равномерное распределение).

Если паттерн зафиксирован, то даже значительные изменения распределения вероятностей (не выводящие за пределы паттерна) не могут сильно повлиять на выбор оптимальной стратегии.

Для простоты будем считать, что проницаемость может принимать только три значения (n = 3). Тогда возможные виды распределения вероятностей (возможные состояния Природы) грубо можно представить в виде следующих четырех векторов:

1151 Г 5 111 p {2 5 21 p /11 11 9 9J 2 1У9J 3 19 У9J 4 13 3 3J координаты которых представляют собой вероятности реализации трех значений проницаемости. Поскольку

то только первые три паттерна являются линейно независимыми. Поэтому паттерн P4 в дальнейшем мы не будем рассматривать.

Еще раз отметим, что нас не должна смущать некоторая кажущаяся произвольность выбора конкретного вида векторов Pk , поскольку принимаемые решения достаточно устойчивы относительно сдвигов и поворотов P , не выводящих их за пределы определенных выше паттернов.

При отсутствии дополнительной информации мы не можем отдать предпочтение ни одному из паттернов Pk (k = 1, 2, 3), поэтому решение принимается игровыми методами (см. предыдущий раздел). Но ситуация начинает изменяться после того, как на данном месторождении начинаются работы по гидроразрыву пласта. Анализ результатов уже сделанных