Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 [ 5 ] 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

/1 л Lk = 4k I -

Поскольку lim Lk =°°, то истинная длина этой кривой бесконечно

велика. При измерении длины с помощью линейки будет определена лишь кажущаяся длина, поскольку какие-то детали фрактальной кривой всегда окажутся меньше самого мелкого деления линейки. Ясно, что значение кажущейся длины растет с ростом разрешающей способности измерительного инструмента. Таким образом, длина фрактальной кривой не поддается четкому определению.

В связи с этим для количественной характеристики свойств фрактала используется размерность фрактала.

Знакомая всем размерность (мы, не вдаваясь в излишние объяснения, будем называть ее топологической размерностью) может принимать только целочисленные значения: линия имеет размерность 1, плоскость - 2, пространство - 3. Топологическая размерность Вт кривой Коха равна, конечно, единице. Но для того, чтобы оценить, как «плотно» кривая Коха заполняет плоскость, может быть введена так называемая размерность Хаус-дорфа-Безиковича Вн (F. Hausdorff, 1918 г. и A. S. Besicovitch).

Легко показать, что

Фп-1 2

где Фn - n -е число Фибоначчи.

Связь чисел Фибоначчи с фракталами проявляется и в алгоритме их вычисления путем бесконечного повторения одной и той же операции суммирования. Числа Фибоначчи также еще появятся в этой главе (см. раздел 1.2.1).

Интересный пример лингвистического фрактала приводит Д. Хоф-штадтер [11, 12]. В переводе М. Эскиной, это - суждение «БОГ, Одолевающий Гения», где слово «БОГ» является одновременно аббревиатурой, составленной из первых букв слов «БОГ», «Одолевающий», «Гения». В свою очередь, таким же образом могут быть расшифрованы слова «Одолевающий» и «Гения». В итоге получится бесконечно разворачивающаяся последовательность суждений, в которых слово «БОГ» оказывается бесконечным сокращением самого себя.

1.1.2. Фрактальная размерность

При рассмотрении фрактальных объектов обычные количественные характеристики (длина, площадь, масса и т. д.) оказываются неприменимыми. Так, длина кривой Коха на k-м этапе построения равна

Практически эта величина может быть определена путем измерения длины кривой с помощью циркуля с уменьшающимся раствором е (см. рис. 1.3).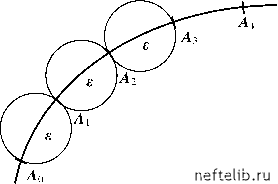

Рис. 1.3. Измерение длин кривых

При этом длина кривой приближенно оценивается как длина ломаной 0А1А2..., где - точки «засечек», произведенных циркулем. Ясно,

что L(e) = N (е)-е, где N (е) - число «засечек». В случае обычных гладких (регулярных) кривых при уменьшении е длина L(e) стремится к конечному пределу L0 - истинной длине кривой (см. рис. 1.4, а). Поэтому в пределе малых е

N (е)= L0

(1.1)

В случае же фрактальной кривой, как уже отмечалось, lim L(ee

(рис. 1.4, б). Оказывается, что для таких кривых L(e)-- при малых е,

откуда

(1.2)

где показатель = 1 + d и называется размерностью Хаусдорфа-Безико-вича.

Так, если с помощью циркуля с раствором е = на кривой Коха, то получится

измеряется дли-

откуда

N(е) = 4к = 3 ln3 N(е) = е in3.

= 00

l(8)

L(£) А

Рис. 1.4. Различные асимптотики L(e) Таким образом, размерность Хаусдорфа кривой Коха равна

Dh = = 1,26.

Этот пример показывает, что фрактальная кривая имеет дробную размерность. Собственно, термин «фрактал» обязан своим происхождением именно этому обстоятельству: латинское слово fractus означает «сломанный», «дробный».

Из (1.1) следует, что для регулярной кривой Вн = 1, т. е. размерность Хаусдорфа совпадает с топологической размерностью Вт.

То, что размерность фрактальной кривой лежит между единицей и двойкой, означает, что она занимает промежуточное положение между линией и плоскостью. В то время как гладкая кривая заполняет в точности одномерное пространство, фрактальная кривая за счет своей бесконечной разветвленности как бы выходит за пределы одномерного пространства.

Размерность Хаусдорфа является количественной мерой того, насколько «плотно» фрактальное множество заполняет окружающее его евклидово пространство.