Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 [ 36 ] 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

компактного пространства М в метрическое пространство N есть гомеоморфизм [4-6]. Компакт М называется классом корректности задачи (2.43).

Задача (2.43), в постановке которой указано, что u принадлежит компакту М, называется корректной по Тихонову (условно корректной). Одним из способов устойчивого решения уравнения (2.43) является минимизация функционала Au - g\ на множестве корректности М ( g - норма элемента g в G). Элемент

uS= Argin fAu - g

называется квазирешением уравнения (2.43) [4]. Предполагается, что вместо g эксперимент дает такое, что g - gg <д; при д - 0, в силу условной корректности задачи, ud - u . Квазирешение определено так, что не обязательно gg N = AM.

На рис. 2.4 изображена ситуация, когда gg AM . В этом случае квазирешение ug есть решение уравнения Aug =д, где cpg - проекция gg на множество N. Часто множество корректности М можно задать с помощью некоторого неотрицательного неоднородного функционала Q:

М = {u G F Q(u )< т •.

В этом случае естественен также альтернативный методу квазирешения подход - минимизация функционала Q(u) на множестве

Au - gg <д.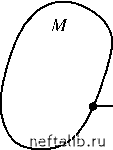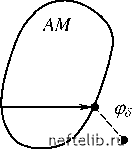

Рис. 2.4. Квазирешение некорректно поставленной задачи

Обычно величина функционала Q (называемого стабилизирующим) характеризует гладкость решения u. Можно показать [5], что этот метод эквивалентен минимизации функционала

Ма[u, gд] = \\Au - ggl2 +а£l(u) (2.44)

на всем пространстве, причем положительный параметр а = а(д) должен, по идее метода, определяться по невязке из условия

где u"; - экстремаль функционала (2.44).

При таких а имеет место сходимость u - u , если 5 - 0. Обо-

значим через Ra(g5) оператор, ставящий в соответствие элементу эле-

мент ua:

Rа(g5),

Ra(g5) называется регулирующим оператором для задачи (2.43) [4-6].

При практическом применении метода параметр а остается, по существу, неопределенным. Обычно проводят расчеты с несколькими значениями параметра а , составляющими геометрическую прогрессию (напри-1 - 2 - 3

мер, 10 ,10 ,10 Из полученных результатов выбирают наилуч-

ший - чтобы решение не было ни слишком сглаженным (слишком большие а), ни слишком «разболтанным» (слишком малые а).

В качестве стабилизатора можно взять, например, выражения типа

п [u (s )]= \ds Z pK (s a к=0

весовые функции, pK (s )>0.

d K u ds K

(2.45)

Отметим, что регуляризующий функционал (2.44) со стабилизатором

Q 2 [u ]

предложен Филлипсом (D. L. Phillips) для случая

c < X < d

2.3. Выбор сложности идентифицируемой модели

Если в задаче меньше трех переменных, это не задача; если больше восьми -она неразрешима.

Из сборника «Физики шутят»

Успех дела зависит от упрощения и от обоснования этого упрощения.

В. Акимов

Априорные сведения о структуре модели изучаемого процесса часто отсутствуют, поэтому вид модели приходится восстанавливать в ходе решения обратной задачи (идентификация в широком смысле этого слова). Как показывает опыт, в условиях неустойчивости большое значение имеет

выбор оптимальной сложности математической модели. Излишнее усложнение модели может привести к неустойчивым алгоритмам идентификации и, как правило, лишает идентификационные модели предсказательной силы.

В качестве простого примера рассмотрим задачу восстановления эмпирической зависимости y = F (x) по экспериментально замеренным точкам {xi, yi}, i = 1, ...,4 (рис. 2.5).

Отклонения экспериментальных точек от графика функции F(x), показанного на рис. 2.5 пунктирной линией, объясняются неизбежными ошибками замеров.

Зависимость y = F(x) можно аппроксимировать следующими моделями возрастающей сложности:

I) у = a x + b;

II) у = a x + b x + с;

III) y = a + b + с x + d,

где коэффициенты a, b, с, d определяются методом наименьших квадратов.

Полученные таким образом зависимости для моделей I и III представлены на рис. 2.5 кривыми 1 и 2 соответственно. Как видно, модель III аппроксимирует зависимость y = F (x) хуже, чем более простая модель I,

особенно при попытке экстраполяции («прогноза») за интервал [x1; x4].

y3 У2

y1 h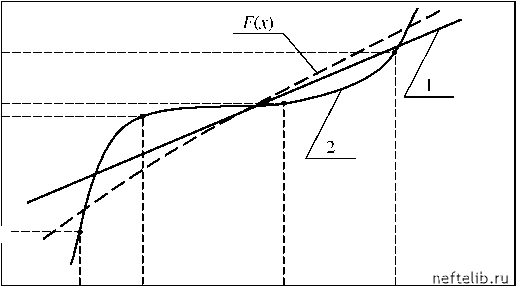

x1 x2 x3 x4 x

Рис. 2.5. Аппроксимация функции полиномами различной сложности

Для слишком сложной модели малые ошибки замеров, незаметные на интервале интерполяции, на этапе прогноза становятся «монстрами», радикально меняющими поведение кривой. По сходному поводу Я. Б. Зель-