Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 [ 32 ] 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

а через

* -1 *

Ф обозначена функция, обратная к Ф .

Обозначая Y1 = Ф

f([) 12С0,

, Y2

получим

Y2 =аГ1, а= 2[В1, т. е. в координатах (Y1, Y2 )экспериментальные данные должны спрямляться, и угловой коэффициент этой прямой определяет коэффициент диффузии D. Результаты обработки экспериментальных данных в координатах (Y1, Y2 )приведены на рис. 2.2, из которого видно, что в данном слу-

чае а = 1, т. е. D = 0,26 • 10 9

Рис. 2.2. Изменение высоты столба жидкости h(t) в

капилляре

На рис. 2.3 приведено сопоставление экспериментальных точек с графиком функции h(t), полученной по формулам решения прямой задачи с определенным выше коэффициентом диффузии D.

Оценивание в нространстве изображений

Если решение прямой задачи получено в пространстве изображений и обращение его затруднительно, то удобнее провести оценивание параметров в в s-плоскости. Пусть y(t) - результаты замеров величины u, u(t, в) - решение прямой задачи, G(s) и V(s, в) - их изображения. Оценивание параметров в пространстве изображений требует минимизации отклонения функции V(s, в) от G(s). Интеграл G(s)= \e-sy(tdt можно вы-

числить любым из способов численного интегрирования. В частности, может быть использована формула

e - sti - e - sti+1

где yi = у (ti), t0 = 0.

s i=0

ti+1 -ti

h, м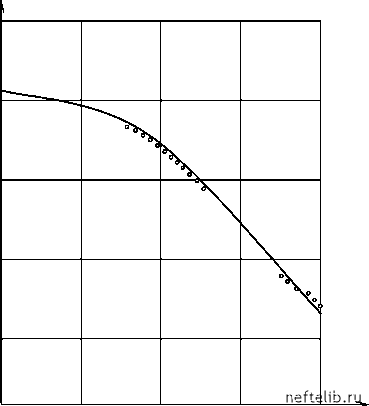

0,25

0,50

0,75

1,00

Рис. 2.3. Результаты обработки экспериментальных данных в координатах (F1, F2 )

Отметим, что метод оценивания параметров, который дает равные веса ошибкам в s-области, не гарантирует равные веса ошибок во временной области. Так, если y(t) = u(t ,в) + е(t), то минимизация выражения

] G(s)-V (s,e) ds

в s-области эквивалентна минимизации \W(t)£(t)dt во временной области,

1 тт./\ exp(-sit)-exp(-s2t) где весовая функция W(t) = ------. В результате ранние моменты времени «весят» больше, чем поздние. Вводя увеличенные веса при меньших величинах s, можно уменьшить вес, придаваемый ошибкам при малых временных.

Чтобы провести оценивание, необходимо использовать дискретные действительные значения переменной s = si (i = 1,2,3,...,N). Для каждого si должны быть вычислены величины G(si) и V(si ,в), и, наконец, выраже-

ние X[g(si)-V(si,в)] должно быть минимизировано по параметрам в. i=1

В ряде случаев вычисления могут быть значительно упрощены за счет рассмотрения асимптотик решения V(s,e) при s - 0 или s - о.

Пример.

Для решения задач оперативного контроля за работой магистральных трубопроводов большое значение имеет вопрос определения коэффициента гидравлического сопротивления по результатам технологических измерений, проводимых в процессе эксплуатации трубопроводов. При этом измеряются давления на входе и выходе трубопровода и расход продукта.

Неустановившееся движение сжимаемой жидкости в трубопроводах описывается известной системой линеаризованных уравнений

+ 2apw,

Эx Эt( ) (2.25)

Э t Э x

где р - давление, w - среднеобъемная скорость, р - плотность жидкости,

2а - коэффициент сопротивления, с - скорость звука.

Задаются следующие начальные и граничные условия:

pwt=0 = 0; pt=0= 0,

= 0(t); px=0 = f0(t). x=0