Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 [ 11 ] 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

климат в своей основе непредсказуемы, так что долгосрочный прогноз погоды невозможен. Чувствительность к начальным условиям, ведущую к хаосу в системе (1.7), Э. Лоренц назвал «эффектом бабочки», поскольку потоки воздуха в атмосфере Земли при такой чувствительности могут зависеть от взмаха крыльев бабочки. Говорят также, что полет мухи в Кембридже может привести к изменению погоды в Индии [15].

Еще одним проявлением аналогии между перемешиванием жидкостей и детерминированным хаосом является следующий удивительный опыт, описанный в книге Дж. Уокера «Физический фейерверк» [22].

Если налить немного глицерина в промежуток между стенками двух коаксиальных цилиндрических стаканов близких диаметров (рис. 1.11), капнуть туда несколько капель краски и повернуть внутренний стакан примерно на 10 оборотов, то краска и глицерин хорошо перемешаются. Однако если после этого вы повернете его на столько же оборотов в обратном направлении, то краска отделится от глицерина и ее распределение будет примерно таким же, как до вращения.

Если же краска и глицерин перемешиваются достаточно долго, то возврат к первоначальному состоянию невозможен.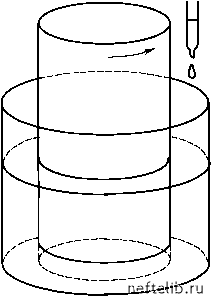

Рис. 1.11. Перемешивание краски и глицерина

Точно так же движение динамических систем, подверженных динамическому хаосу, можно обратить на малых масштабах времени, когда неустойчивость не успевает себя проявить.

Так, если после нескольких соударений бильярдного шара со стенками (см. рис. 1.7) заставить его двигаться с той же скоростью, но в обратном направлении, то весьма вероятно, что шар повторит свою траекторию

и вернется в исходную точку. Если же число соударений при прямом движении столь велико, что шар «забывает» о своем первоначальном положении, то обратить движение уже не удастся, как не удастся собрать капли краски после достаточно долгого вращения стакана в описанном выше опыте.

Примеры проявления детерминированного хаоса, рассмотренные

выше, связаны с расхождением траекторий по закону eA, где A - показатель Ляпунова. Для таких систем непрерывная зависимость решений от начальных условий нарушается лишь при t -оо . В работе [23] хаос такого рода предложено называть «слабым» (weak) хаосом. Там же отмечено, что возможны хаотические движения, связанные с нарушением непрерывной зависимости решений от начальных условий за конечное (и даже сколь угодно малое) время.

Для иллюстрации этого вида неустойчивости рассмотрим уравнение Лапласа

Э 2 u д 2

Э t2

с начальными условиями

t > 0,

(1.8)

Эта задача имеет тривиальное решение u = 0. Если же вместо (1.8) рассмотреть слегка отличное (возмущенное) начальное условие

Э u -4П

= cos nx,

то получим

u = f (x, t ) =1 e cos nx sh nt

Легко видеть, что

- 0 при n - о, т. е. новое начальное усло-

вие стремится к невозмущенному, однако новое решение при сколь угодно малом времени может (за счет члена sh nt ) сколь угодно сильно отличаться от невозмущенного решения u = 0.

Хаос, связанный с неустойчивостью такого типа, называется «сильным» (strong) и может проявиться, например, при распространении возмущений в средах, нелинейные свойства которых приводят к смене гиперболического типа уравнений движения на эллиптический [23]. В частности, это возможно в эластичных средах, имеющих падающий участок на зависимости напряжения от растяжения.

1.2.2. Хаос и размерность систем

Возможность проявления детерминированного хаоса в динамических автономных системах вида (1.6) существенно зависит от их размерности. Можно показать, что в двумерном пространстве хаотические траектории невозможны, поскольку в нем могут существовать только такие аттракторы, как точки равновесия, бесконечность и предельные циклы. Допустим, например, что диссипативная система имеет (рис. 1.12) два инвариантных множества - точку равновесия P и предельный цикл C [15]. (Напомним, что инвариантными называются множества точек в фазовом пространстве, по которым, раз попав на них, все остальное время движется изображающая точка.)

Траектория, начинающаяся внутри кривой С, остается там навсегда, так как в противном случае она пересекла бы эту кривую, что, по теореме единственности, невозможно. Той же теоремой запрещены и самопересечения траектории движения. Тогда единственно возможными остаются движение к точке Р (см. рис. 1.12, а) или движение к предельному циклу С (см. рис. 1.12, б).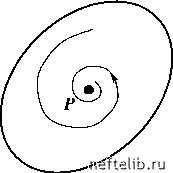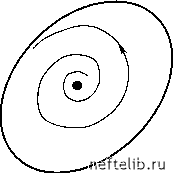

Рис. 1.12. Точка равновесия и предельный цикл

Для трехмерных систем и систем более высокого порядка ограничения, накладываемые теоремой единственности, оказываются более слабыми, поскольку траектории имеют возможность избегать друг друга, выходя из плоскости в пространство. Благодаря этой гибкости оказывается возможным одновременное осуществление двух условий стохастичности:

а) все (или почти все) соседние траектории внутри некоторой области разбегаются;