Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 [ 12 ] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

Если давление меняется незначительно, то

y(p)dp = A idp. (П. 2. 21)

ЧЕИТеЛЬНО, ТО

-глгорЧ-™* (П. 2.22)

где Zcp - среднее значение z в пределах изменения давления.

Для более точных расчетов, разумеется, интеграл (П. 2.21) следует вычислять соотвйтственно точнее. Для идеального газа, приводя к атмосферным условиям уат, Рат, при температуре течения Т получаем

L = J=.RT, (II. 2. 23)

P = d2 +const. (П. 2. 24)

Для однородной упругой капельной жидкости, ввиду малого изменения у, у (р) в (11.2.17) можно считать обычно практически постоянной у{р)~Уо- Тогда

P = Yop-(-const. (П. 2. 25)

При постоянных к, ц, пренебрегая массовыми силами, из (И. 2.14) получаем

= уР- (П. 2.19)

Потенциал, как и функция Р, определяется с точностью до аддитивной (т. е. прибавляемой) произвольной постоянной. Поэтому интегралы в (П. 2. 12) или (П. 2. 18) могут оставаться неопределен-

ными или записываться в виде J, где ро -любое давление, в частно

ности нуль.

Найдем вид функции Р для газов и упругой капельной жидкости. Для газов, особенно углеводородных, уравнение состояния у = = у (р, Т) часто берется в виде

-у=2ДГ, (П. 2. 20)

где R - газовая постоянная; Т - абсолютная температура; z = = Z f , - так называемый коэффициент сверхсжимаемости,

\ Ркр J кр )

определяемый по эмпирическим формулам или графикам; Гкр, ркр - критические температура и давление. Для идеального газа, следующего уравнению Клапейрона, z = l. Для Р получим

§ 3. Замечания о системе уравнений для общего случая неизотермической фильтрации

В большинстве случаев движение природных жидкостей и газов в их естественных коллекторах - пористых средах, слагающих продуктивные пласты, - предполагается изотермическим, хотя известно, что при атом температура изменяется, правда, обычно незначительно. Примером является описываемый во всех курсах термодинамики классический эффект Джоуля - Томсона.

В связи с развитием современных, весьма точных методов термометрии пластов и скважин представляет интерес составление полной системы уравнений, связывающих скорости, давления и температуры жидкости и пористой среды. Информация, доставляемая в виде термограмм пластов и скважин, может оказаться полезной при изучении их фильтрационных параметров.

Пз работ, выполненшлх в этом направлении, следует отметить исследования Э. Б. Чекалюка, посвященные задаче о связи между гидродинамическими и термическими параметрами фильтрационных потоков, и предложенные им методы использования этой связи [5, 6].

Большой интерес также представляет задача о нагнетании горячей жидкости, газа или пара в пласт для повышения нефтеотдачи и улшения проницаемости призабойной зоны. "

Для простоты будем предполагать пористую среду неизменяемой и однородной. Замкнутая система уравнений для давления р, вектора скорости "ш, плотности Q или объемного веса у и температур Т ш Ti жидкости и пористой среды может быть получена, как и во всех задачах механики сплошных сред, при помощи основных фундаментальных законов сохранения, справедливых для любой системы материальных тел и точек, - закона сохранения массы, закона изменения количества движения и закона сохранения энергии.

Обычно в фильтрационных задачах ввиду весьма малых скоростей жидких частиц в основной области течения в уравнениях движения и энергии инерционными членами и кинетической энергией принято пренебрегать. Мы этого пока делать не будем и постараемся для общности получить полную систему уравнений, пригодную для исследования движений, где скоростями частиц пренебрегать нельзя, например, при притоке газа п скважвну через перфорационные отверстия, когда условия истечения приближаются к критическим и скорости струек газа в отверстиях могут быть сравнимы с звуковыми, а такнсс для других случаев течевия в пористой среде, где необходим учет инерционных членов.

В качестве примера можно указать недостаточно еще исследованный круг задач о распространении колебаний в пористых средах, заполненных жидкостью или газом. В этих задачах, представляющих интерес для развития сейсмиче-сквх, акустических и других аналогичных методов исследования и разведки нефте-, водо- и газоносных пластов, учет инерционных членов имеет принципиальное значение при расчете скорости распространения того или иного вида механических колебаний. При отбрасывании инерционных членов акустические скорости получаются бесконечными. В одних задачах это обстоятельство не вносит сколь-лпбо сутцестпетюй погрешности, в других же, если, например, требуется более точно исследовать процессы, возникающие в начальные моменты после прихода фронта волны давления, необходимо учитывать конечное значение скорости звука.

Полная система уравнения для общего случая движения в пористой среде сжимаемой или несжимаемой вязкой жидкости принципиально может быть построена, как упоминалось выше, путем надлежащего осреднения уравнений Навье - Стокса и уравнения энергии, что ло сего времени пока что пе сделано.

Вместо этого, следуя И. Е. Жуковскому, согласно сказанному выше в § 2 можно рассматривать фильтрационный поток как идеальную жидкость и силы фильтрационного трения отнести к объемным силам сопротивления. Тогда можно воспользоваться хорошо известными уравнениями движения идеальной жидкости, приведенными в любом современном курсе гидродинамики.

газовой динамики или механики спловшых сред [13, 14, 15], добавив к реально существующим объемным силам фиктивные указанные выше силы сопротивлений.

Для практических приложений целесообразно иметь полную систему уравнений для трубки тока с заданным законом изменения площади фильтрации / (s). Подробный вывод для этого квазиодпомерного течения приведен ниже, после чего уравнения, выражающие рассматриваемый закон, выписываются непосредственно в координатной форме.

Применим законы сохранения к потоку жидкости, текущей внутри трубки тока, выделенной в фильтрационном потоке и ограниченной двумя поперечными сечениями Д и (рис. II. 2). Для простоты будем считать положение трубки тока в пространстве фиксированным. Как и выше, под действительной скоростью жидкой частицы будем подразумевать величину w/т, где ш - вектор скорости фильтрации; т - порпстость.

Напомним общий метод записи изменения какой-либо величины Ф, связанной с потоком жидкости.

Рассматриваются два положения частиц в моменты t и t -\- А t (рис. II. 2). Очевидно, изменение рассматриваемой величины Ф можно записать так: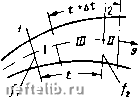

Рис. II. 2.

АФ= [(Фш)( +д( + Ф„]- [(ФшЬ + Фг] = = Ф11-Ф1+(Фт)( + д1-(Фт)<-

(II. 3.1)

Члены Ф, Ф определяют значение величины Ф в объемах частиц, вышедших из сечения /г и вошедших в сечение Д за время At, (Фщ )< > (Ф11)(ц.д( -ее значения в общем объеме III в моменты t и t-\-At.

Переход к пределу при Д г -> О и сокращение на d г дают соответственно конвективную производную рассматриваемой величины, обусловленпую переносом частиц, и локальное ее изменение в единицу времени, обусловленное нестационарностью процесса.

Аналогичным образом производится запись для движущегося объема произвольной формы.

§ 4. Закон сохранения массы фильтрационного потока

Закон сохранения массы и веса будет иметь вид:

Gi-G2 = JmydV,

(II. 4.1)

где Gi и Ga - весовые расходы соответственно в сечениях и Д; V-объем трубки тока между сечениями /i и Д.

Если сечения бесконечно близки, то dK = /(s)ds и формула (П. 4.1) принимает вид:

G (S, t)-G(s+ds, t) = -i/(s)ds

G(s, t)-

G(s, t)-

ds

dt dG

dG d (m Y) ~ ds - dt

(II. 4. 2)

t. e. мы получили обычное уравнение неразрывности.