Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 [ 95 ] 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

Отсюда

М ГП /д п п 1 Ро(До. )-Рст(До)

{VIII. 6.20)

«о С)

2л kh

Hi(<)

Ро(Д,.0-Рст(До) J д,. (VIII.6.21)

/{Д„. Д„, Hi) J

В зависимости от условий задачи можно выбирать интегральное соотношение в виде {VIII. 6. 17) или {VIII. 6. 21), в дополнение к которым следует использовать связь между давлением и расходами {VIII. 6. 15).

Ниже рассмотрено несколько примеров нестационарной фильтрации упругой жидкости с неподвижными и подвижными граничными условиями.

2. Ограничимся простейшей аппроксимацией F (г, До, ДО в виде линейной зависимости

{г. До, Д1) = {Д1-г)/{Д1-Д„). {VIII. 6. 22)

Согласно {VIII. 6. 16) и {VIII. 6.17)

fir. До, R.)-Tdr= -(-bln-l) , {VIII. 6.23)

/ {До> До> Д1) =

Д1 / До

-blnf-lH

Д1 1„ Д1

Д1 -До \ Д1 J /(г, Д„, Д1)гг = Д + -;(ДоД1 +

In-J-1, {VIII. 6. 24)

Но С)

1 r2

3 о 2{Д1-Д„) "о" Д„ •

{VIII. 6. 25)

По методу последовательной смены, полагая F (г, Rg, Ri) = 1, получаем более грубое приближение

/(г. До. R,)f = ln,

f(Rg, Д„, Д1) = 1п

Д1 Д„

Й1 Hi

/{г, Д„, Ri)rdr Г

{VIII. 6.26) {VIII. 6. 27) 28)

Рассмотрим два примера. I. Нагнетание расхода Qo (О скважину постоянного радиуса До=соп51 в неограниченном пласте. Нулевые начальные условия Рст{г)=0, Qct = 0.

Условие {VIII. 6.17) принимает вид:

2л kh > 2л kh

1 + «о«1 , К iK

3 2{Д1-Д„) Д„

или, обозначая

W 10]

Ч 2.0

"о

(VIII. 6. 29)

= (Q+?)+4--2()°e- (VIII. 6. 30)

Q {t)R 1? 0 о

П 120

16 ISO

20 200

Рис. VIII. 9. Графики зависимости депрессии от времени при притоке с постоянным дебитом к скважине конечного радиуса в неогра-нчченном пласте: пунктир - по точному решению, сплошные линии - по расчету методом интегральных соотношений.

Отсюда можно найти g для заданного t. Давление на скважине согласно (VIII. 6.18) и (VIII. 6. 24) меняется по закону

(VIII. 6. 31)

При Qo{t) = const = Q„, из (VIII. 6.30) находим

3 2{Q~\)

In Q.

(VIII. 6. 32)

Раскрывая неопределенность, из (VIII. 6. 32) получаем т = О при е = 1.

На рис. VIII. 9 приведена кривая т = т (е) согласно (VIII. 6. 32). Задаваясь различными значениями т, по кривой рис. VIII. 9 можно найти соответствующие значения Q, а затем по уравнению (VIII. 6. 31) ро (t).

Для сравнения с точным решением, приведенным в книге Маскета [6], выражающимся трудно вычисляемым несобственным интег-ралом

2Cot nkh

1 -е

-22 X

г[/,(2) + Г;(г)]

{/i, У1 -функции Бесселя действительного аргумента первого и второго рода первого порядка), на рис. VIII. 9 приведены кривые отношений

(f = nkhpJ2Q„ii

(VIII. 6. 34)

по точному уравнению (VIII. 6.33) (фм) и по уравнениям (VIII. 6.31) и (VIII. 6. 32):

2яуо 0

яз khp„ я2

е 1пе-1

(VIII. 6. 35)

2Жкк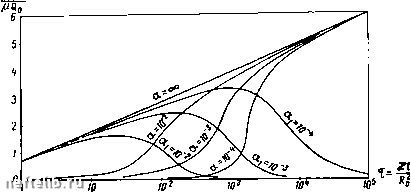

Рис. VIII. 10. Графики зависимости депрессии от времени при притоке к скважине конечного радиуса в неограниченном пласте при различных

законах отбора.

Как видно из рис. VIII. 9, точная и приближенная кривые хорошо совпадают.

На рис. VIII. 10 показаны три серии кривых, соответствующих следующим законам изменения дебита Q (t), закачиваемого в скважину постоянного радиуса в неограниченном пласте:

1) Q («) = const =Q„-постоянный темп нагнетания, дебит постоянный;

2) Q(i) = Qo(l -е~"") (Qo = const соответствует а = оо) -постепенное увеличение темпа нагнетания, дебит возрастает от нуля, приближаясь к предельному значению Q„\

3) С (t) = Q„e~"i -постепенное уменьшение темпа нагнетания, дебит уменьшается от начального значения Q„, приближаясь в пределе к нулю.

На графиках рис. VIII. 10 по- оси абсцисс отложено в логарифмическом

масштабе безразмерное время т = - , по оси ординат-безразмерное да-

вление в виде отношения

(VIII. 6. 36)