Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 [ 25 ] 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

Полученная из F функция Fi определяет некоторый плоский фильтрационный поток на плоскости %. Очевидно, изучив первый поток F, можно легко изучить поток F\ {%).

Таким образом, задаваясь той или иной преобразующей функцией Z = Z (), из одного потока F (z) плоскости z можно получить бесчисленное множество других потоков на плоскости Как принято говорить в теории функций комплексного переменного, функция z = = Z реализует конформное отображение плоскости z на плоскость .

Для решения задач интерференции скважин в качестве исходного потока удобно взять рассмотренное выше течение к скважине, эксцентрично расположенной в круговом пласте, являющееся вместе с тем, как было показано ранее, течением между равнодебитными источником и стоком.

Применение метода конформного отображения позволяет получить решения ряда задач интерференции скважин значительно быстрее, нежели методами, основанными на прямой суперпозиции источников и стоков.

Метод конформных отображений в настоящее время широко применяется во многих физических и технических задачах. Ряд примеров можно найти в книге М. А. Лаврентьева и Б. В. Шабата [1]. К задачам гидротехнической фильтрации - расчетам обтекания подземных контуров плотин фильтрационным потоком - систематическое приложение метода конформных отображений было сделано впервые акад. Н. И. Павловским [2]. При помощи этого метода удается решить ряд плоских задач напорной и безнапорной, фильтраций. Подробное изложение и ряд примеров приведены в [Лт. II. 2, 3, 4, 5], а также ниже в § 3, 4.

§ 3. Вывод некоторых формул для притока к скважинам при помош,и конформного отображения

Предположим, что на плоскости комплексного переменного z = = X -\- iy дано некоторое течение с комплексным потенциалом F(z). Введем новое комплексное переменное 1, = I, + i r\, связанное со старым переменным z зависимостью z = z или = (z).

Отделяя в функции z = z () действительную часть от мнимой, получаем

z{l) = z{l + i)=x{l, ц) + 1у{1,ц),

откуда

х = х{1,ц), у = у{1,у\), .JJJ 3

1==1(х,у), ц = ц(х,у).

Уравнения (III. 3. 1) устанавливают соответствие между точками плоскостей и Z. В зависимости от того, однозначна или многозначна преобразуюш,ая функция z = z (t,), каждой точке плоскости соответствует одна или несколько точек плоскости z.

Точно так же каждой линии одной плоскости соответствует одна или несколько линий на другой плоскости. Таким образом, линиям тока и эквипотенциалям, т. е. сетке течения одной плоскости, будет соответствовать вполне определенная сетка течения на другой плоскости. При этом, разумеется, сами значения потенциала скорости Ф и функции тока будут одинаковыми на соответствующих друг другу линиях обеих плоскостей.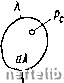

©

Рис. III. 4.

Производная dzldt, есть также некоторая функция комплексного переменного, вполне определенная в соответствующих друг другу точках обеих плоскостей z и . Это означает по самому определению производной, что предел отношения

lim -пг = lim . /

Д£0 AS Д,0;дг1,0 А+гДЛ

не зависит от закона стремления к нулю отрезков А и Ат]. Отсюда следует, что в каждой точке плоскости % и соответствующей (или соответствующих) ей точке плоскости z отношение соответствующих бесконечно малых отрезков dz и постоянно. Но из каждой точки плоскости можно провести бесконечное множество отрезков dt,i, d2, ... Им будут соответствовать на плоскости z бесконечно малые отрезки dzi, dz2, также исходящие из точки плоскости z, соответствующей рассматриваемой точке плоскости (рис. П1. 4).

Так как в каждой точке есть вполне определенная вели-

чина, то

dz..

(HI. ,3. 2)

Из (III. 3. 2) следует пропорция

Аргумент дроби равен разности аргументов числителя и знаменателя. Но argdzi -это угол между направлениями элемента dzi и осью X.

Таким образом,

arg dzi - arg dz = arg d%i - arg d%i,

T. e. углы между отрезками dzi, dza и отрезками dt,!, d% равны.

Поэтому преобразование z(Q или (z) называется конформным, так как оно сохраняет подобие бесконечно малых элементов в соответствующих точках.

Пусть на плоскости z имеется скважина радиусом Гс-На плоскости t, ей будет соответствовать скважина радиусом Qc, причем так как радиусы скважин обеих плоскостей можно считать очень малыми по сравнению с размерами областей течения, то на основании формулы (III. 3. 2)

г с =

Qc, Qc =

(HI. 3.3)

Покажем теперь, что при конформном отображении дебиты скважин - стоков или источников - сохраняются на обеих плоскостях. Для этого окружим скважину на плоскости z произвольным замкнутым контуром I, которому на плоскости % будет соответствовать также замкнутый контур %. Пусть dn w. dl - элементы нормали и касательной для контура / на плоскости z и соответственно d\ dX - для контура "к на плоскости t,.

Тогда абсолютная величина дебита скважины на плоскости z выразится интегралом по замкнутому контуру

\dl\

(П1.3.4)

так как Wn=----составляющая скорости фильтрации по нормали к контуру.

Но по смыслу конформного преобразования, сохраняющего подобие бесконечно малых элементов в соответствующих точках обеих плоскостей, согласно формуле (III. 3. 2) имеем

I dn \dl I

dl dz

\dX\.

(IH.3.5)