Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 [ 35 ] 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

Приближение заключается в том, что для точек контура питания принимаем и те же расстояния Rk до скважин.

Если контур питания достаточно удален, то расстояние Rk можно принять одинаковым для всех скважин, учитывая, что оно находится под знаком логарифма.

Уравнение (IV. 3. 5) и будет (га -Ь 1) уравнением.

Таким образом, плоская задача интерференции при удаленном контуре питания сводится к решению алгебраической системы уравнений (IV. 3. 2) - (IV. 3. 5), являюпщхся уравнениями первой степени с соответствующим числом неизвестных.

Эту систему можно упростить, исключив константу С. Вычтем каждое из уравнений (IV. 3. 2) - (IV. 3. 4) из последнего уравнения (IV. 3. 5). Тогда получится система из п уравнений.

Вычитаем сначала первое уравнение (IV. 3. 2) из (IV. 3. 5):

9i In

2, 1

3, 1

(IV. 3.6)

Вычитая второе уравнение, получаем

Фк-Фс2 =

9iln

"1,2

-,,1п + ,з1п

+ ...

-g„ln-) (IV. 3. 7) 1,2

Фк-Фсп = - (?1 In

92 In

Ди 2, п

g,ln

-Яп In

Гс п

(IV. 3.8)

При помощи последней системы уравнений можно решать задачи двоякого рода: или находить депрессию при заданном дебите, или, если заданы депрессии, то, решая эту систему, получить значения дебитов. Положительные значения дебитов будут для скважин-стоков - эксплуатационных, отрицательные - для скважин-источников - нагнетательных. После того как дебиты найдены, пластовое давление в любой точке определяется из формулы (IV. 3. 1), причем результат тем точнее, чем дальше эта точка отстоит от контура питания.

Эти формулы дают полное решение задачи. Они годятся для пластов с удаленным контуром питания, потому что для пластов с близким контуром питания уравнение (IV. 3. 5) будет недостаточно точным.

Покажем в заключение, как определяются скорости фильтрации в любой точке пласта, где находится группа скважин.

Нетрудно видеть, что если результирующий потенциал получается алгебраическим суммированием потенциалов каждой скважины в отдельности, то результирующая скорость получится геометрическим суммированием скоростей, определяемых каждой скважиной в отдельности.

Рассмотри.м группу скважин. Контур питания предполагается достаточно удаленным.

Требуется найти потенциал и скорость фильтрации в точке М, отстоящей от наших скважин на известных расстояниях п, rj,..., г„ (рис. IV. 5, а).

Если бы эксплуатировалась только одна первая скважина, то скорость фильтрации была бы направлена по радиусу п и равнялась бы

и>1 =

2л ri

Скорости Ш2, Шз, . . ., Wfif определяемые второй, третьей и т. д. скважинами, равны

W2 = -

2л Гг

2л Гз • • •

Wn - -

2л Гп

Остается сложить эти скорости, определяемые каждой скважиной в отдельности, по правилу параллелогралпяа или по правилу многоугольника, чтобы получить результирующую скорость (рис. IV. 5, б), w = п + W2 + Шз--...+а%.

Зная вектор скорости фильтрации, можно найти истинную скорость движения жидкости в этой точке по формуле V ~ и/т.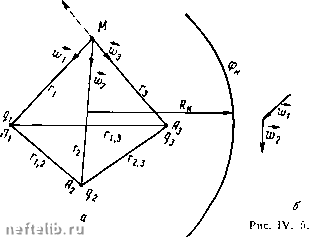

Вернемся к решению задачи о скважине в пласте с прямолинейным контуром питания (см. рис. IV. 6).

Найдем скорость в какой-либо точке М пласта.

Если расстояние а от контура питания до скважины велико по сравнению с расстоянием точкп М до скважины, то скважину можно не отражать. Если а мало, то нужно зеркально отразить реальную скважину С в контуре питания, причем дебит изображения С будет - q.

При вычислении скорости нужно учесть скорость, определяемую действительной скважиной и ее изображением.

Скорость, определяемую скважиной-стоком, обозначим вектором wi (рис. IV. 6), а скорость, определяемую скважиной-изображением, которая является источником, обозначим через u-.

Результирующая скорость ш будет равняться их геометрической сумме: -

- W1 W2, причем

2л г,

Ш2 =

2л Г2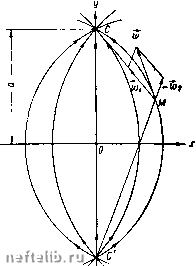

Рис. IV. 6.

Найдем направления скоростей точек, лежащих на оси х, у = 0- Легко видеть из рис. (IV. 6), что результирующая скорость ш для этих точек будет паправлена перпендикулярно оси х.

Контур питания

§ 4. Приток к бесконечньш цепочкам и кольцевым батареям скважин

Перейдем к многорядным батареям скважин. Исследование задачи об интерференции скважин в пласте с удаленным контуром питания показывает, что в общем случае приходится решать столько уравнений, сколько имеется скважин.

На месторождениях имеются десятки и сотни скважин. Очевидно, решать десятки или сотни уравнений даже первой степени невозможно без применения быстродействующих вычислительных

устройств. Приближенное решение задачи получается следующим образом.

При рациональной системе разработки скважины располагаются обычно в виде рядов, расставленных вдоль контура нефтеносности и контура питания.

Пусть внутри области питания вдоль нескольких линий расположены скважины. Эти линии называются часто батареями или рядами скважин (рис. IV. 7).

Можно считать, обычно без большой погрешности, дебит скважин в каждом ряду одинаковьш, если, конечно, в каждом ряду скважины находятся в одинаковых условиях.

Дебиты же скважин в разных рядах будут отличаться друг от друга.

Наибольший дебит будет иметь первый ряд, ближайший к контуру питания. Поэтому число одновременно работающих рядов редко бывает больше двух-трех и последующие ряды включаются по мере приближения контура нефтеносности. Когда вода подошла к первому ряду, он выключается и включается один из следующих рядов и т. д.

В этом случае число неизвестных уменьшается от числа скважин п до числа рядов iV" (причем iV" обычно не превосходит 2, 3, 4), а это уже гораздо более простая задача.

Будем исходить из формулы (IV. 3. 1) для потенциала при работе группы скважин

Рис. IV. 7.

Ф = -

2„ 2 qilnr + C,

где п - число всех скважин.

Последовательное расположение точки М на контуре каждой скважины позволило составить систему (IV. 3. 2)-(IV. 3. 4), (п -j- 1)