Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 [ 92 ] 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

§ 5. Расчет радиального притока упругой жидкости по методу последовательной смены стационарных состояний

Значительно лучшие результаты дает метод последовательной смены стационарных состояний при радиальном притоке упругой жидкости к скважине.

Рассмотрим радиальный приток упругой жидкости к скважине из пласта мош,ностью h (рис. VIII. 8, а, б).

Когда из скважины начали отбор, вокруг нее образовалась воронка депрессии, которая теоретически захватывает весь пласт. Мы будем считать, что воронка депрессии распространилась на какую-то конечную длину, причем радиус R (t) этой воронки депрессии условный.

Нетрудно видеть, почему для радиального движения метод последовательной смены стационарных состояний будет давать лучшие результаты, нежели для прямолинейного. При прямолинейном движении кривая распределения давления аппроксимируется двумя прямыми линиями (см. рис. VIII. 6).

При радиальном движении кривая распределения давления аппроксимируется логарифмической кривой. Расхождение между двумя кривыми оказывается меньше, чем расхождение между прямой и кривой.

Найдем убыль жидкости из цилиндрического кольцевого

элемента пласта внутренним радиусом г {гс<г< В (t)), мош,ностью h, толщиной dr, считая, что первоначально скважина не эксплуатировалась и пластовое давление было всюду постоянным и равным (рис. VIII. 8).

Объем элемента пласта равен 2л rh • dr. Первоначальный вес жидкости в этом элементе пласта равен 2лгЛ (my)„dr. Вес жидкости в нем в данный момент 2л rhm у. Убыль веса жидкости в элементе равна разности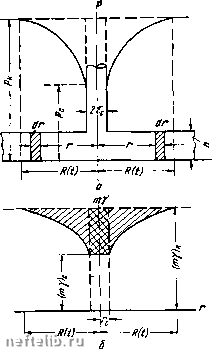

Рис. VIII. 8.

Весовое количество жидкости, отобранное из пласта, равно

к (О

G = / 2ягк1ту)н - ту] dr.

(VIII. 5. 1)

Чтобы воспользоваться этим уравнением, нужно знать, как изменяется ту в пласте. Примем, что ту изменяются по законам стационарного движения

Когда движение стационарно, давление р в окрестности скважины распределено по логарифмическому закону согласно уравнению

Р = Рн -

Рн-Ро rc<r<R (t), (VIII. 5. 2)

Д(0 с

где R (t) - радиус воронки депрессии в данный момент t.

Очевидно, произведение ту, линейно зависящее от р, будет распределено по такому же закону:

ту = {ту)к- ("-V)K-(y)c АЖ (vn.5.3) ]п -

/ \ (ту)к~(ту)с , R(t)

(тау)к-тау дш "-7-

Подставляя это выражение в формулу (VIII. 5.3), получаем G = j 2nrh In dr. (VIII. 5. 4)

Интеграл в уравнении (VIII. 5.4) легко берется интегрированием по частям. Получим

л (О

rlndr =

=-щ-[{ту)к - {ту)с]

1п ilili

/ 2

с

InRit)- +[lnrc-~f)\. (VIII.5.5)

Раскрывая скобки, после сокращений будем иметь

R(tl

2 Гс

Почленно поделив на 1п-, окончательно получим

G = nhl{m y)„ - {т у)с]

21п л (i)/rc

- Гс

{Vin.5.6)

Это количество жидкости извлечено непосредственно из пласта вокруг скважины (показано штриховкой на рис. VIH.S, б).

При вычислении полного количества жидкости, отобранной из пласта, необходимо учесть также жидкость, отобранную из скважины при снижении в ней давления с начального рк до забойного Рс.

Для реальной скважины это дополнительное количество жидкости ничтожно мало, но для укрупненной скважины, моделирующей целое месторождение, оно может оказаться существенным. Это дополнительное количество жидкости показано двойной штриховкой на рис. Vni.8.

Полное количество жидкости, извлеченной из пласта и скважины, обозначим Go-

Оно будет равно

Go = яА[(ту)„ -(ту)с]

л («)--с

- "с

2 In

+ п rji [{тп у)к - {т у)с]

Go = я ft [пг у)„ - {т у)с]

R{t)~rc

2 In

Учитывая, что

Rjt)

(VIII. 5. 7)

{т y)„ - (m y)c = {т у\ - ,

и подставляя значение этой разности в уравнение (VIII. 5.7), окончательно получаем

Рк-Рс R"(n~rl

Go = Я ft (m y)o

К Z\nR{t)lrc

(VIII. 5.8)

Найдем теперь объем жидкости, соответствующий этому весовому количеству. Он получится, если разделить вес Go на ус