Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 [ 63 ] 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131

жидкостей (X = 0); 3) по схеме жестких трубок тока, причем спектр трубок тока был взят соответствующим начальному моменту движения i ~ 0. Во всех случаях были приняты одинаковые переьады давлений между контуром питания радиусом Rk и забоем скважины радиусом тс, а также X - -0,5, Rk - 10\

= 10. с

Результаты расчета приведены на ри. VII. 9. Кривая 1 получена интегрированием на электронной вычислительной машине уравнения движения, кривая 2 - по схеме «разноцветных» жидкостей и кривая 3 - по схеме жестких трубок тока. Видно, что в данной задаче метод жестких трубок тока несколько преуменьшает влияние различия вязкостей.

Рис. VII. 8. Графики для расчета времени прорыва воды в скважину, эксцентрично расположенную в круговом пласте, при различных соотношениях вязкостей.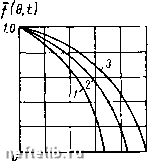

Рис. VII. 9. Сопоставление различных методов расчета времени прорыва.

Время прорыва к скважине по методу жестких трубок тока оказывается для приведенного выше примера согласно рис. VII. 9 на 25-30% больше действительного, что дает представление о точности этого метода. При других соотношениях вязкостей и различном эксцентрицитете, как было исследовано А. М. Власовым [12], расчеты на ЭВМ и по методу жестких трубок тока для времени прорыва к скважине дают расхождение как существенно меньше, так и больше - в пределах 0±56%. А. М. Власов [12] предложил формулу ддя поправочного коэффициента, позволяющего уменьшить это расхождение до 5-7%.

Следует отметить попутно, что иногда расчеты на ЭВМ с методом жестких трубок тока сопоставляются в предположении, что вся область течения от контура питания до скважин заполнена только одной жидкостью - водой или нефтью [13].

По самой же идее метода жестких трубок тока, изложенной в [Лт. II. 9], следует брать за исходную систему тпубок тока, существовавшую в момент г=0.

Конфигурация этой системы, в дальнейшем считаемая неизменной, должна быть определена с учетом того, что в начальный момент существует не одна жидкость, а две. При расчетах же по формуле (VII. 3. 7) следует предположить, что эта начальная система трубок заполнена только одной жидкостью, и уже после этого определять сначала скорости 2 " давления Р2-2 Д"" одножидкост-

ной системы, а затем из формулы (VII. 3. 7) скорость границы раздела ii-. для двухжидкостной.

Следует отметить также, что везде выше рассматривалось так называемое «поршневое» вытеснение. В действительности, о чем более подробно будет сказано в главе IX, одна жидкость вытесняется обычно не поршневым образом, а с образованием переходной зоны, т. е. зоны смеси, так как полное вытеснение по ряду причин не реализуется, К таким причинам в первую очередь следует отнести капиллярные эффекты, согласно которым вытеснение происходит не одинаково в поровых каналах различных размеров. При образовании же переходной зоны, т. е. при реально суш,ествующей неполноте вытеснения, картина линий тока, как показывают эксперименты [14], остается во времени практически неизменной.

§ 5. Вытеснение нефти водой из трубки тока переменного сечения

С задачей о вытеснении нефти водой приходится встречаться при проектировании разработки нефтяных месторождений, когда нужно учесть стягивание контура нефтеносности, а также при расчетах деформации водо-нефтяного контакта. Аналогичные вопросы нозни-кают и при эксплуатации газовых месторождений с краевой или подошвенной водой.

Чтобы охватить по возможности все многообразие частных случаев, рассмотрим следующую задачу. Трубка переменного сечения заполнена пористой средой, в которой одна жидкость вытесняет другую, например вода вытесняет нефть (см. рис. VII. 3). Пусть в одном сечении трубки, рассматриваемом как контур питания в водяной части, известно давление рк, в другом сечении трубки - в нефтяной части, рассматриваемом как скважины, известно давление рс- Требуется рассчитать продвижение границы раздела, предполагая, что эта граница является некоторой поверхностью.

В действительности граница раздела вследствие капиллярности и других причин будет размыта, но мы будем предполагать, что она четко очерчена и вытеснение одной жидкости другой происходит «поршневым» образом.

Заметим, что если во втором сечении (в скважинах) будет задан отбор жидкости, то движение границы раздела определяется из простых геометрических соображений, так как объем, образованный движением границы раздела, будет равен объему отобранной жидкости.

Прежде чем рассматривать двухжидкостную систему, напомним, как решалась задача о движении однородной жидкости в трубке переменного сечения (§ 3, гл. I) / = / (s).

Рассмотрим трубку переменного сечения, где в одном сечении давление Pi, а в другом р2 (рис. VII. 10). Для упрощения задачи будем пренебрегать эффектом силы тяжести. Плотности обеих жидкостей считаются одинаковыми.

Решение задачи получается непосредственно из закона Дарси. Скорость фильтрации w равна

к dp

W =---f- .

р ds

Объемный расход соответственно равен

(VII. 5. 1)

kf{s)

Знаменатель последней формулы можно назвать фильтрационным сопротивлением и обозначить его через R:

(VII. 5. 2)

В таком случае формула (VII. 5. 1) будет записана в виде, аналогичном закону Ома:

р1-р2 R

(VII. 5. 3)

Рис. VII. 10. Схема движения в трубке тока переменного сечения.

Этой формулой воспользуемся для решения нашей задачи, когда движется не одна жидкость, а две, причем одна вытесняет другую.

Очевидно, формулу (VII. 5. 2) можно применить в отдельности к каждой из областей, занятых водой и нефтью, но для этого надо знать давление р на границе раздела.

Это давление, вообще говоря, переменная величина.

Расход каждой жидкости, воды ия нефти, можно записать так:

Рк-Р Р -Рс

(VII. 5.4)

kt(s)

kf(s)

где Лв, Цн - соответственно вязкость воды и нефти; I - вся длина трубки.

Чтобы избавиться от неизвестного промежуточного давления р, сложим числитель и знаменатель по правилу производных пропорций. Тогда р сократится, и мы получим

Рк -Рс

(VII. 5. 5)

kj(s)

kf{s)

Последняя формула представляет собой не что иное, как закон Ома для последовательного соединения двух проводников. В этом случае сопротивления складываются, что здесь и получилось.