Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 [ 102 ] 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

12. Katz D. L. and Coats K. H., 1965. Underground storage of fluids. Ulrich Book, Inc. An Arbor, Michigan.

13. Scelkacev V. N. and Lapuk B. В., 1953. Underground hydroulics. Technical Editions, Budapest.

14. Reiss L. H., 1976. Reservoir engineering of fractured reservoir. French Institute of Petroleum, Paris.

15. Baker W. /., 1955. Flow in fissured reservoir. Proceeding Fourth World Petroleum Congress, Section П/Е. p. 379-393.

16. Kazemi H., 1969. Pressure transient analysis of naturally fractured reservoir with uniform fracture distribution. Soc. Pet. Eng. J., p. 451-458.

17. Warren J. E. and Root P. J., 1963. The behaviour of naturally fractured" reservoir. Soc. Pet. Eng. J., p. 245-255.

18. DeSwaan H., 1975. Analytical solution for the determination of naturally fractured reservoir parameters by well tesling. SPE Ventura meeting, California..

19. Birks J., 1963. Coning theory and its use in predicting allowable producing, rates of wells in a fissured limestone reservoir. Iranian Petroleum Institute, Bull. 12&13, p. 470.

20. Saidi A. M. and Martin R. E., 1965. Application of reservoir engineering in the development of Iranian reservoirs. Paper presented to the E. C. A. F. E.. Symposium of Petroleum, Tokyo, No. 10-20.

21. Muskat M. 1937. Homogeneous flow in porous media. McGraw Hill, New York.

22. Ofstad D. R., 1976. Research project B5020: Fractures reservoir behaviour. Univ. of Trondheim.

Глава 7

ТЕЧЕНИЕ ЖИДКОСТИ К СКВАЖИНЕ В ТРЕЩИНОВАТОЙ ПОРОДЕ С ДВУМЯ ВИДАМИ ПУСТОТНОСТИ

Пласт, пустотное пространство которого представлено межзерновой пористостью, изучается при упрощающем предположении, что-он однороден и что основные его физические свойства, такие, как пустотность и проницаемость, всегда связаны определенной зависимостью.

Трещиноватый пласт характеризуется дискретностью свойств или параметров каналов вследствие наличия двух видов пустотности рис. 7.1). Матрица обладает более мелкими порами (пустотами) и отличается значительной вмещающей способностью, но низкими фильтрационными свойствами. Трещинная система, наоборот, характеризуется низкими емкостными, но высокими фильтрационными свойствами.

Методы разработки таких пластов отличаются от методов, применяемых для разработки коллекторов с межзерновой пустотностью. В ряде работ [1]-[5] уточнены различные методы разработки на основе упрощенных моделей пластов. Целью этих работ был расчет характеристик течения в особых условиях резкой неоднородности коллектора. Использование одной или нескольких предложенных моделей дает большой объем информации, в том числе на основании интерпретации данных, полученных в пластовых условиях. Эта информация включает результаты расчета пустотности и проницаемости областей пласта с разными видами пустотнос-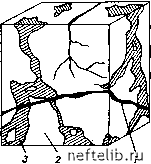

Рис. 7.1. Образец реальной трещиноватой породы продуктивного пласта [1.] / - трещина; 2 - матрица; 3 - каверны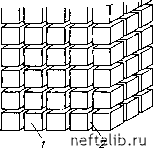

Рис. 7.2. Идеализированный трещиноватый пласт [1]. / - матрица; 2 -трещина

тп при определенных условиях, оценку распределения и густоты трещин и т. д.

В этом разделе рассматривается главным образом модель Уоррена - Рута, а также другие модели [2], [4]-[6].

В модели Уоррена - Рута трещиноватый пласт схематизируется одинаковыми прямоугольными параллелепипедами, разделенными прямоугольной сетью трещин (рис. 7.2). Считается, что движение жидкости к скважине происходит по системе трещин, а матрица непрерывно питает всю систему трещин при условиях квазистационарного течения. Для описания нестационарного течения выведена зависимость, учитывающая влияние давления и представляющая собой функцию двух безразмерных параметров и со. Эти параметры характеризуют взаимосвязь между двумя областями пласта с разными видами пустотности. Величина x выражает интенсивность перетока жидкости между двумя областями пласта, а (о - относительную емкостную характеристику этих областей. Зависимость изменения давления от логарифма времени (для случая падения п восстановления давления), полученная в результате обработки данных по модели Уоррена - Рута, на графике выражается двумя параллельными линиями вместо одной, как это наблюдается для пласта с межзерновой пустотностью, причем для трещиноватого пласта характерно некоторое запаздывание во времени.

Разница между опережающей и запаздывающей параллельными линиями зависит от относительной емкостной характеристики трещин (о, а период неустановившегося давления между опережающей и запаздывающей линиями будет функцией коэффициента перетока X между областями пласта. Наклон параллельных линий является прямой функцией фильтрационной характеристики системы трещин, не зависящей от межзерновой пористости (см. гл. VI). Модель Уоррена - Рута обеспечивает детальное понимание механизма фильтрации в трещиноватом пласте.

Основные допущения построения модели Уоррена - Рута аналогичны допущениям модели Оде [2]. Единственное различие их заключается в определении двух типов пустотности. Из анализа исходных данных о трещиноватом пласте Оде сделал вывод о том, что вмещающая способность двух систем (трещин и матрицы) в общем настолько схожа, что после переходного периода от нестационарного течения к стационарному наступает период, когда трещиноватый пласт ведет себя как пласт с межзерновой пустотностью. Поэтому модель Оде рассмотрена вместе с моделью так называемого обычного пласта.

В модели Полларда [3] изменение давления в переходном периоде рассчитывается как результат взаимодействия трех областей, которые развиты в трещиноватом пласте. Первую область образует система трещин вокруг скважины, вторую - вся трещинная система пласта вдали от скважины и третью - матрица, которая питает трещины. Две последние области представляют собой трещиновато-матричную систему, подобную той, которая упоминалась выше. Но вначале падение давления бывает связано с системой трещин, окружающих скважину, затем с системой трещин всего пласта и только на третьей стадии-с падением давления в матрице. После того как снизилось давление в матрице и она начала питать трещины, процесс течения быстро становится квазистационарным. Падение давления в скважине (как результат последовательных событий) можно представить в виде ряда, состоящего из членов с временной экспонентой.

Уточненная зависимость логарифма падения давления от времени позволяет рассчитать объемы трещин и матрицы. Модель Полларда, хотя и не учитывает радиальную геометрию течения и сводит задачу к простому процессу расширения, в некоторых случаях дает приемлемые результаты. Использование ее для расчета различных параметров по аналогии с пластами с межзерновой пустотностью в ряде случаев может быть успешным, но часто приводит к значительным погрешностям.

В модели Каземи [4] трещиноватый пласт аппроксимируется слоистой системой, состоящей из тонких с высокой проводимостью слоев, которые моделируют трещины, чередующихся со слоями большой мощности с низкой проводимостью и высокой емкостной характеристикой, представляющими матрицу. С помощью численного интегрирования изменения давления в скважине во времени эта модель дает результаты, удовлетворительно совпадающие с результатами модели Уоррена - Рута для случаев равномерного распределения трещин и при сочетании высокой вмещающей способности матрицы с возможностью интенсивных перетоков жидкости пз матрицы в трещины.

Модель де Сваана [5] описывает неустановившееся течение жидкости на основании предположения, что матричные блоки представляют собой бесконечные плиты правильной геометрической формы или сферические блоки. Позднее эта модель была усовершенствована Наджуриета [6] для целей интерпретации данных ис-