Главная  Переработка нефти и газа 

Скачать 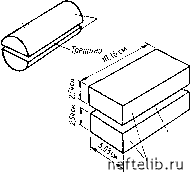эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 [ 153 ] 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Матрица

Рис. 9.63. Цилиндрическая и прямоугольная модели, использованные X. Каземи [15] в экспериментах

Трещина

<Энагн.б возможно извлечение до 60% нефти к моменту прорыва воды (рис. 9.61). Кроме того, при малых CR{CR = Qfib) независимо от величины CR или при низких его значениях (С/? = 0,1) независимо от величины Снагн.б результаты процесса вытеснения также оказываются лучшими (кривая е на рис. 9.62). в. Зависимость накопленной добычи воды от накопленной добычи нефти подтверждает, что невысокие значения Рнагн.б и CR приводят к большим значениям нефтеотдачи за счет увеличения периода безводной добычи (рис. 9.62).

Матрица

9.5.2.3. Модель Каземи [15]

Экспериментальные исследования, проведенные Каземи [15] на моделях с искусственными трещинами, были выполнены на разрезанных цилиндрических образцах и прямоугольных блоках, имеющих горизонтально простирающуюся трещину (рис. 9.63). Размеры цилиндрических образцов составляли: 7,62 см в длину и 2,54 см по диаметру. Прямоугольные образцы имели размеры: 10,16 см в длину с квадратным (5,08x5,08 см) или прямоугольным (5,08х х2,54 см) сечением. Образцы полностью насыщались нефтью, соленой или пресной водой. Опыты проводились при низких и высоких скоростях перемещения воды в трещинах, и при этом были сделаны следующие наблюдения:

а) при низких скоростях перемещения фронта воды в трещинах (0,308 м/сут) превалируют капиллярные силы, и фронт вытеснения перемещается в блоках матрицы быстрее, чем фронт вытеснения в трещинах;

б) при высоких скоростях продвижения фронта воды в трещинах (1,54 м/сут) и низком капиллярном давлении прорыв воды наблюдается в трещиноватых породах значительно раньше, чем в породах, не имеющих трещин;

в) нефтеотдача за счет капиллярной пропитки очень тесно связана с нефтеотдачей при заводнении;

г) только в тех случаях при продвижении воды по трещинам, когда блоки на 100% насыщены нефтью, наблюдалась некоторая задержка впитывания, проходившего достаточно эффективно. Ничего подобного не отмечалось в тех случаях, когда блоки матрицы характеризовались некоторой начальной водонасыщенностью.

9.6. Теория нефтеизвлечения из единичного блока

В предыдущих разделах рассматривались процессы извлечения нефти из единичных блоков, причем особое внимание обращалось на физические аспекты вытеснения нефтей при капиллярной пропитке, т. е. при вытеснении нефти водой, или при дренировании, т. е. при вытеснении нефти газом.

Единичный блок при этом рассматривался как однородный, и поэтому весь процесс вытеснения описывался уравнениями, пригодными для описания процессов фильтрации в однородных породах.

в действительности задача значительно более сложная, так как в трещиноватых породах-коллекторах блоки матрицы могут обмениваться жидкостями только через прилегающие к ним трещины. Таким образом, вдоль направления вытеснения вытесняющий агент стремится перемещаться по трещинам с большей скоростью, чем по блокам, благодаря высокой неоднородности, создаваемой наличием сети трещин. С другой стороны, непрерывное проникновение вытесняющей жидкости из трещины в блоки приводит к снижению разницы в скоростях движения вытесняющего агента в обеих средах: трещинах и пористых блоках.

Взаимная обусловленность процессов вытеснения нефти из блоков и трещин требует нового подхода к трактовке вопросов, связанных с вытеснением нефти из блоков матрицы в трещиноватых породах-коллекторах. Этот подход основан на рассмотрении трещиноватых пород-коллекторов как целого. Так, аналитическое исследование трещиноватых пород-коллекторов основано на континуальном подходе («влоЛСении» друг в друга сред с различной пустотностью) в формулировке Баренблатта [18]. в численных моделях, тем не менее, возможно представление трещиноватого коллектора в дискретном виде, т. е. в виде отдельных трещин и блоков матрицы. в этом разделе рассматривается только континуальное приближение, в то время как численные методы включены в следующую главу.

9.6.1. Континуальное приближение Баренблатта [18] для случая совместного течения несмешивающихся жидкостей в трещиноватых породах-коллекторах

Континуальное приближение для случая однофазных течений в трещиноватых породах-коллекторах (см. гл. 7) обобщено на случай двухфазных течений несмешивающихся жидкостей. Уравнения фильтрации выписываются для течения каждой фазы через составную среду трещиноватого резервуара - трещины и пористые блоки; переток вытесняющей жидкости из трещин в блоки и истечение вытесняемой жидкости из блоков в трещины описывается чле-

нами источник - сток в уравнениях сохранения массы в соответствии с законом, определяющим вытеснение флюида из блока, т. е. функцией капиллярной пропитки.

9.6.1.1. Вытеснение нефти газом

Уравнения течения при вытеснении нефти газом из трещиноватого коллектора сформулированы Баренблаттом. Уравнения неразрывности для нефти (индекс н) в блоках (индекс 1) и трещинах (индекс 2) записываются следующим образом:

1Ф1Рн (i) -Hi]+div (Л) t «н1 J +«:=о,

[Ф1Рн (2) Sh2] + div Грн (Р,) Мн21 + «: = 0.

di д

(9.87) (9.88)

Уравнения неразрывности для газа (индекс г) в блоках и трещинах записываются так:

[Ф1РГ (1) -п + Ф1РН (i) R {Pi) 5hi] +

+div рлл) «н +«:=о,

(9.89)

div [р, (Р,) «г2 J - «: + -- [ФгРг (2) г2 + ФгРн (2) R {Р2) S,] = О,

(9.90)

где R - растворимость газа; и* - функция, определяющая обмен жидкостями между двумя средами, которую Баренблатт предложил записывать в следующем виде:

"н =

"г -

sKiKoi (St)

Рн(Л)Л-Рн(2) dP;

p. Рг

\P„{P,)dP,- P,{P,)dR

(9.91)

p. Pl

pAPi)dPi- Pr{P.)dP,

-0 0

(9.92)

где s аналогично коэффициенту уравнения (9.90). Решения этих уравнений неизвестны.

9.6.1.2. Вытеснение нефти водой

Боксерман, Желтов и Кочешков [6] представили уравнения сохранения массы воды и нефти в трещинах следующим образом: