Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 [ 46 ] 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

4.3. Проницаемость

Основная концепция определения проницаемости, установленная для обычного порового коллектора, остается в силе и для трещинных коллекторов. Но при наличии двух типов пустот (поры матрицы и трещины) можно выделить проницаемости матрицы, трещин и всей системы.

Такое выделение проницаемостей может вызвать некоторую путаницу. Особенно это касается трещинной проницаемости, которую можно интерпретировать как проницаемость единичной трещины, системы трещин, а иногда и некоторого трещиноватого объема. Поэтому ниже будут детально рассмотрены различные определения проницаемости.

4.3.1. Истинная проницаемость трещин тр

Истинная проницаемость трещин ассоциируется с проводимостью, замеренной при течении жидкости через единичную трещину или систему трещин, вне зависимости от окружающих пород (матрицы). По сути дела, это проводимость единичного канала (трещины) или группы каналов (сети трещин). В этом случае сечение потока определяется только площадью пустотного пространства трещины (без площади матрицы, окружающей трещину).

По упрощенной схеме блока, когда трещина параллельна направлению течения (рис. 4.7, трещина /), количество флюида, протекающего через трещину, определяется уравнением

9тр =

12,4. /

12,а ;

(4.9)

Если единичная трещина образует угол с направлением потока (рис. 4,7, трещина 2), то поперечное сечение его (аЬ) будет оставаться неизменным, а трещина будет проектироваться на направление течения:

9тр = аЬ

12,и.

(4.10)

с другой стороны, исходя из закона Дарси, для полного сечения потока (Л = аЬ) количество флюида можно выразить следующим образом:

Рис. 4.7. Блок матрицы с единичной трещиной.

Для трещины / а=0, для трещины 2 афО: А - полное сечение потока

Напрабление

течения флюида

TP p fjrp АР

q = A

Сопоставляя уравнения (4.11) и (4,10), получаем

Дтр =

- cos ос.

(4.11)

(4.12)

Для системы трещин с одинаковой ориентацией (из определения в гл. 2 следует, что систему трещин образует группа параллельных трещин) истинная проницаемость выражается следующим уравнением:

тр =

L 1

Для сети трещин, образованной системами трещин а, р, ... (каждая со своей ориентацией трещин), истинная проницаемость [6] равна

Кгр = C0S4 2 + " 2 +• •

L 1 1

4.3.2. Общепринятое выражение проницаемости трещин Дтр

Истинная проницаемость трещин, рассмотренная выше, не учитывает общий объем породы, в которой находятся единичная трещина или группа трещин, в то время как для общепринятой трещинной проницаемости (основанной на классическом определении Дарси) трещина и окружающий ее объем породы (блоки) образуют единую гидродинамическую систему. Это означает, что сечение потока (см. рис. 4.7) равно не А = аЬ, а

= ah.

и, следовательно, 1

П - л тр. пл Ч - бл-

(4.14)

(4.15)

Если приравнять уравнения (4.15) и (4.9) и подставить результат в уравнение (4.12), то получим:

аЬ ah

= к:

i2/i

(4.16)

4.3.3. Проницаемость трещинно-матричной системы

Проницаемость трещинно-матричной системы может быть получена простым сложением проницаемости матрицы К.м и трещин Ктр: /С,р.„л = /См + /С.р. (4.17)

рис. 4.8. стандартный цилиндрический образец керна.

Трещины: а - ориентированные; 6 - хаотич-

Если уравнение (4.17) рассматривать применительно к блоку, показанному на рис. 4.7, то-станет ясно, что общая проницаемость блока будет зависеть от

направления потока. Любое изменение направления течения изменит величину Kip, поскольку она зависит от угла между ориентацией трещины и направлением течения.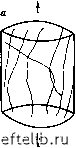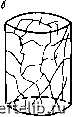

4.3.3.1. проницаемость, определенная по керну

При использовании стандартных цилиндрических образцов керна и обычных приборов проницаемость по уравнению Дарси определяется выражением

тр. пл

(4.18)

которое соответствует общей проницаемости системы, а не проницаемости только матрицы или только трещин. На оценку величины /Стр. пл существенное влияние оказывает также ориентация трещин относительно направления течения. Так, проницаемость керна с ориентированными трещинами (рис. 4.8, а) в случаях горизонтального и вертикального потоков будет различной, поскольку в керне преобладает вертикальная ориентация трещин. В то же время, если трещины ориентированы хаотично (рис. 4.8, б), величина Ктр.пл, определенная по уравнению (4.18), будет характеризовать проницаемость всей трещинно-матричной системы независимо от направления течения. Этот последний случай менее вероятен.

Следует заметить, что обычно в трещиноватом пласте-коллекторе довольно трудно получить представительные значения трех видов проницаемости: Кобщ, Ктр и Кк- В определенных идеализированных условиях измерения керна (см. рис. 4.8, а) при вертикальном и горизонтальном течениях могут дать соответственно значения

Кверг = Км-Ь Кгр И Кгор = Км-

4.3.3.2. проницаемость, определенная по результатам испытания скважин

В случае установившегося радиально-симметричного притока флюида в скважину проницаемость рассчитывают по классическому уравнению