Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 [ 54 ] 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Пустотность в случае хаотичного распространения трещин:

577,9 = 0,052 %.

1880 1,2XI,5 log(2000/0.1) q

0,47 100

= 5,2x10-* =

Идеализированный смоделированный коллектор. Если полученные результаты преобразовать для трещиноватого пласта-коллектора, идеализированного по модели 4 (см. табл. 4.6) с целью определения размера блока а и раскрытости трещин b по Кчр и Фтр, то лолучим

b = 1/-j = 1/=162 мкм.

У 4,16X10-* фтр V 4,16X0,052

= = Vl,04Xo!o523 = 62,4 см.

Новая густота трещин равна

Л.тр = - = = 0.0162, I/cm. а 62,4

Трещинная пустотность, определенная по уравнению, будет такой же, что и установленная при исследовании скважин:

= -1><1 = 0,052 o,i. юоа 100X62,4

Если эти данные применить для модели 6 по той же методике, то получим:

j2l = l/= 140 мкм; У Фтр 5,55 У 0,052 5,55

а = i/TjT = /il-L . 80,8 см. К 0,62 К 0,05? 0,62

Новая густота трещин

™ = - = - = 0,0248. " а 80,8

Проверяя значение Фтр по параметрам а п.Ь, получим

Фтр = 0,03 Ш = 0,052 %.

\ а J

Проницаемость матрицы К. Для условий испытаний при установившемся притоке проницаемость трещин определяется по коэффициенту продуктивности трещинной системы. При этом могут возникнуть вопросы - питает ли матрица трещины и каков должен

быть порядок величины проницаемости матрицы для обеспечения такого притока?

Обращаясь к тому же примеру расчетов для различных режимов залежей, получаем дебит одного блока (qбл i) для фазы простого расширения по условиям модели 6 (табл. 4.6):

и, следовательно,

Число блоков

Коэффициент продуктивности всего пласта-коллектора равен (/)обш="(/)бл1=12,

Как видим, в случае упругого режима даже очень низкая проницаемость матрицы может свободно обеспечить высокую продуктивность. При размере блока а=0,8 м, радиусе дренирования 500 м получается, что проницаемость, равная 5-10~® мкм, обеспечивает продуктивность 1000 мсут/МПа при р,= 1,017 мПа-с и h = a= = 80 см:

ш00х0,8-х 1,017 1 5. 127:5002 0,8

Гравитационный режим. Как будет рассмотрено в главах 9 и 10, при гравитационном режиме можно получить уравнения только для дебита скважин (а не для коэффициента продуктивности). Первоначальный приток при гравитационном режиме (за счет впитывания воды) для единичного блока, мгновенно погруженного в воду, выражается уравнением

Если считать, что Ay= (ув-ун)=0,2х10-2 кг/см; a = /i = 0,8 м; Вн= 1,2; р,н= 1,5 мПа-с, то

Сг.бл1= (0,8 X -0,2 X 10-x0,0864 = 0,061 Дм/сут. 1,2 x 1,5

Для каждого ряда блоков площадь при радиусе дренирования 2000 м равна

ряд = (2x10)2= 12,56x10» м2.

Тогда число блоков равно «=12,56x106/0,64 = 19,62 X 10*.

При таком числе блоков одного ряда дебит в м/сут будет равен «г.ряд = Сг.ряд X /г = 0,061 X 19,62 X 106 = 1,2 X юе j

Дебиты свыше 1000 м/сут и выше 10 000 мсут будут получены, если первый ряд блоков полностью заводнен и проницаемость в первом случае выше 0,001 мкм, во втором - выше 0,01 мкм. Если обводнены десять рядов, то такие дебиты будут получены при матричной проницаемости, равной соответственно 0,0001 в первом случае и 0,001 мкм во втором.

Необходимо помнить, что и при гравитационном режиме в случае низкой проницаемости матрицы в трещиноватом пласте-коллекторе при наличии системы с двойной пустотностью могут наблюдаться обильные притоки жидкости.

4.4.2.2. Связь Ф и /С в породах матрицы

Связь между пористостью Фм и проницаемостью Км пород матрицы определяется классическим уравнением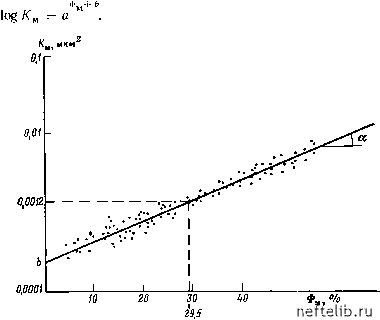

(4.44) (4.45)

Рис. 4.21. График зависимости /См-Фм по кериу