Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 [ 119 ] 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

0,0007

О 1 2 3 <> 5 В 1 S S 10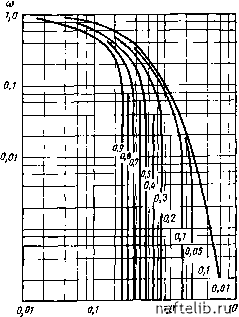

0,001

0,0001

Рис 7.22. Кривые зависимости Рнс. 7.23. Кривые зависимости со-(Рви)з для

ш-(Fbu)o для различных зна- различных значений &.t*l(tp+&.t*s).

ченнй &.t*li(p + M*s) [9]. Шифр кривых - значения M/if+M,) Шифр кривых - значения Д<*/(р+

Используя пример расчета № 2 (см. рис. 7.16) и задаваясь безразмерным временем, равным 2,99-10-, которое рассчитано по точке перегиба кривой давления

1350

450 ООО-f- 1350

= 2,99-10-*,

можно найтн А5=1350 с.

Зная, что ш = 0,03, из рис. 7.22 находим значение {Fbu)o0,16. Далее, используя уравнение (7.126), где 9 = 23 и ДГ5 = 1350 с, получаем:

0,16

23 X 1350

=5,15-10-6.

Величины x и W оказались такими же, какие были получены путем прямых определений в примере расчета № 2.

7.3. Обсуждение метода Полларда

Метод Полларда, основанный на зависимости логарифма давления от времени, требует прежде всего уточнения основных данных о пласте.

7.3.1. Обработка данных

Перепад давления рассчитывается по отношению к статическому давлению и, следовательно, при замеренном давлении Ртр.скв суммарный перепад давления равен

АРобщ = Рпл-Ртр.с«в. (7.130)

По диаграмме logAPoOm-определяется наклон прямой линии mi, как показано на рис. 7.24. При экстраполяции прямой линии до А/=0 получается значение Ср, а давление находится по уравнению (7.66), которое описывает прирост давления в матрице в зависимости от времени:

AP, = Cpe-"

Данное уравнение описывает закон восстановления давления в матрице.

Разница давлений АРобщ-APi представляет собой общее восстановление давления в системе трещин:

АР2.з=АР„ощ-АР.. (7.131)

Из зависимости logAPip - At определяется наклон прямого участка кривой Шг, как показано на рис. 7.24. Экстраполяция кривой до А/ = 0 дает величину Dp, тогда восстановление давления в трещинах всего пласта можно выразить следующим образом:

АР,р = АРг.з-АР, = £)pe-"=

Поскольку, как видно на рис. 7.24,

fJp = Лр Ср, то в случае Up>Dp щр

что определяет давление в сети трещин вокруг скважины. ю

« yC~~~naSedsHus системы

рР.,--ае." ---

Рис. 7.24. Пример расчетов с использованием модели Полларда, основанной иа зависимости log АР-St "

7.3.2. Основные параметры

7.3.2.1. Объем пор матрицы

В соответствии с классической зависимостью между объемом, сжимаемостью и падением давления

Эту же зависимость можно выразить через скорость перетока: Объем матрицы с учетом уравнения (7.66)

Kм=-. (7.132)

7.3.2.2. Объем трещин

На основании той же зависимости

, dt ,

Объем трещин с учетом уравнения (7.67)

СтР L>p iCp

7.3.2.3. Пустотность матрицы Фм и трещин Фтр

В упрощенном виде

Ум-г Утр

ф (7.134)

Vm + Ктр

7.3.3. Дополнительные параметры, определяемые ПО аналогии с параметрами пористой среды

К дополнительным параметрам, которые могут быть получены по аналогии с параметрами пористой среды и рассматриваются как ориентировочные, относятся следующие параметры:

а) коэффициент продуктивности (для трещинной системы)

р/=2£а = 2£а; (7.135)

АР Dp