Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 [ 98 ] 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

рис. 6.23. кривые зависимости критической и безопасной высот конусов hs и йг от дебита Q.

2-h.

В.кр

3-h.

г.безоп

AQ, + BQ •Рг)

; 7,44-10"» +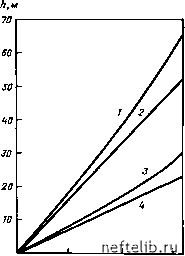

зооа

6.9(рн-

+ 5,46-10-8 Q

где Q - в см/с; /г - в м.

Результаты расчетов приведены на рис. 6.23 в виде графиков зависимости h=f{Q), причем хорошо видно различие hs и Лг для критических и безопасных условий отбора нефти.

2. Дебит скважин в зависимости от времени. По данным табл. б.З о продвижении ВПК и ГНК во времени находятся Яв и Яг. Работающая продуктивная толщина определяется из уравнений йв = НТПЖ - Яв со стороны водяного конуса (графа 4 табл. 6.3) и /1г=ВТПЖ -Яг со стороны газового (графа 5 табл. 6.3).

Зная hs и /ir, определяют по графику на рис. 6.23 максимальный безопасный дебит без риска образования водяного (графа 6) и газового (графа 7) конусов. Величина допустимого дебита, а точнее его изменения во времени, приводится в графе 8 табл. б.З.

Пример. На 5-м году разработки месторождения Яв = 23 м и Яг=20 м. Из этого следует, что потенциальная высота водянога конуса 57 м, а газового - 30 м. По рис. 6.23 находим, что Сбезоп= = 2800 мсут в случае образования водяного конуса и Сбезоп= = 3200 м/сут в случае образования газового конуса.

7000 гооо Q, мУсут

6.3. Течение газа в трещиноватом пласте-коллекторе

6.3.1. Основные концепции и результаты экспериментов

Течение газа через трещины представляет особый интерес, так как очень многие газовые залежи приурочены к трещиноватым пластам. Задача о течении газа в трещинах решалась математическим путем. Полученные результаты показали, что характер течения в трещине существенно зависит от критических условий, в том числе от распределения давления между входом в трещину и выходом из нее.

Другим подходом к решению подобной задачи была аналогия с течением жидкости (табл. 6.4). В соответствии с этим допущением результаты экспериментов по фильтрации жидкости были скоррек-

уравнения течения жидкости

№ уравнения

уравнения течения газа

Ко уравнения

примечание

12х dx tfl dP

" 12х dx 1 = 6/Re

Re= рб£)/2(х

b dP

fv dx

г;=4,7

dp dx

.1 = 0,056/Re/*

(6.32)

(6.32) (6.28)

(6.33)

Alp da;

*3 p„r dP

I2(i. Alp x = 6/Re

Re = x = -

dP dx

v = AJ

(6.34)

( 2RJ

dP dx

\ щ i 9=4,7 6x

b ( 2RJ \

dP V

, dx

i = 0,056/Re/*

(6.75)

(6.75) (6.76) (6.77)

(6.78)

(6.79)

(6.79)

Ламинарное течение

Параметры, определяющие характер течения (фильтрации)

(6.80)

Турбулентное течение

тированы с учетом специфических характеристик газа, таких как сжимаемость и плотность.

Уравнения, полученные в разделе 6.1, описывающие основные параметры фильтрации жидкости при ламинарном и турбулентном течении, были пересмотрены для случая течения газа (табл. 6.4).

Уравнения (6.32), (6.33), (6.34) были модифицированы путем выражения плотности газа как функции среднего давления

Р = (Л + Р,)/2.

где Pi и Рг - давление соответственно на входе и выходе из нее.

Подставляя в основные уравнения течения жидкости (см. табл. 6.4) при ламинарном и турбулентном течении, а также в выражения числа Рейнольдса плотность газа

и выражая расход как функцию различной раскрытости b единичной трещины

q= bxlxv

получим основные уравнения течения газа.

На специальных моделях проводились эксперименты по определению предела применимости этих уравнений, при этом менялись величины как расходов, так и раскрытости трещин, их длины и ширины.

Вначале эксперименты проводились при больших значениях раскрытости трещин, меняющихся в пределах 0,45-б мм, и при постоянной их длине 10 см. Использовался азот при средней температуре 20°С со следующими характеристиками: р=1,125х XlO-5 г/смЗ; ji2o° с=1,75-10-2 мПа-с; М = 28,02 г/моль.

На следующем этапе использовалась та же модель с раскрытостью трещин от 0,011/до 0,0314 мм. Причем проводились очень точные замеры давления. Результаты замеров представлены на рис. 6.24 и 6.25. Диаграммы на этих рисунках, построенные в логарифмических координатах, показывают измененне величины расхода q в зависимости от градиента давления dPjdx. и коэффициента i. в зависимости от числа Рейнольдса Re. В обоих случаях использовалось понятие среднего значения расхода, которое полу-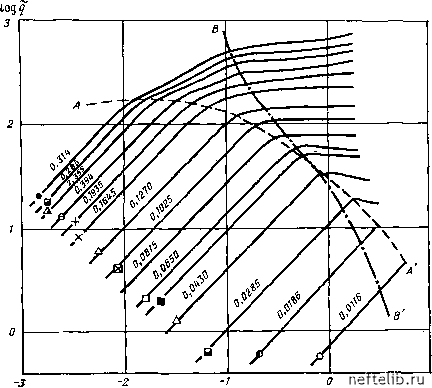

Lg dP/dv

Рис. 6,24. Кривые зависимости q-dP/dx при течении газа через трещину с малой раскрытостью (0,0116<Ь<0,314 мм). Шифр Кривых - значения 6, мм; q в смс; dPIdx в ат/см