Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 [ 104 ] 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

dv, (7.14)

где Jo - функция Бесселя первого порядка нулевой степени; V - переменная интегрирования.

7.1.2. Метод Уоррена-Рута [1]

Уоррен и Рут [1] представили в несколько уточненной постановке решение той же задачи. Они учитывали сжимаемость трещин, но пренебрегали движением жидкости в блоках матрицы. Соответствующие уравнения для радиального течения, как следует из уравнений (7.6), будут иметь вид

Ф.С,

дРг , SKi

dt

l-t I г dr

d I dP,\

-{P,-P,) = Q.

(7.15)

7.1.2.1. Падение давления в бесконечном пласте

Рассматриваются следующие начальные и граничные условия: = 0; Р,(г, 0) = Р2(г, 0) = Ро;

К дР

г = Гскв. «7 = - 2i:r<.„b - -, когда t > 0;

[1 dr

Г оо; Р, = Р = О, когда t > 0.

(7.16)

Уоррен и Рут [1] определили соответствующие безразмерные

параметры и представили уравнения (7.15) и условия (7.16) в безразмерной форме:

Pg = {2T.KhIqii) [Ро - Р (г, 01; Гб = г/Гс„в;

= К4 /[(С.Ф, + С,Ф,) xrL]; (7.17) X = аКЛкв/К2, = Ф.,С2/(Ф1С, + ФСа).

Уравнения (7.17) в сочетании с граничными условиями (7.16)

дают: )

dP6,

Г6 dr6 \ drQ

(1-ш)--Х(Рд,-Рб,)=0.

--(1 ш) = 0; dt dt

(7.18)

<б = 0; 61 = 62 = 0;

Гд = 1; DPJdr - 1, когда > 0; (7.19)

/• -> оо = Рб2 = о. когда / > 0.

решение, полученное с помощью преобразования лапласа, имеет вид

где l - оператор обратного преобразования лапласа;

() = П7Г=ТГГ1Г (7.21)

[(1 - «) s + x]

ло и К\ - модифицированные функции бесселя второго порядка соответственно нулевой и первой степени.

трансформирование уравнения (7.20) в общем случае не может быть получено аналитически. однако асимптотическое решение для малых значений s/(s) может быть получено при рассмотрении только первых членов ряда по функциям бесселя, т. е.

/CoVsns) =-т-1п

(7.22)

КЛУМЩ\= (7.23)

Vsf{S)

где у - 0,5772 - число эйлера.

такая аппроксимация годится только при значениях параметра 15/(5) меньших 0,01, что обычно соответствует значениям времени б>100 или, более точно, 6>100(fl при ж1 и /б>100я-1м

для (1)<1.

с учетом уравнения (7.20) трансформированное уравнение (7.21) будет иметь вид

62 (1. U) = 4- f0.80908+ln /с -ь Ei \-] -Ei(~ -]] ,

(7.24)

где Ei - интегральная экспоненциальная функция, определяемая выражением

i X) = - --du. (7.25)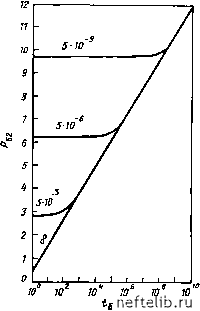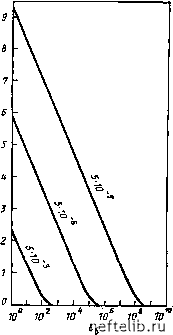

Рис. ,7.3. Графическая иллюстрация решения Уоррена-Рута [I] (уравнение (7.24)) д.чя бесконечного пласта w = 0 и некоторых конкретных значений Я. Шифр кривых - значения %

а. Обсуждение графического представления

Решение уравнения (7.24) в графической безразмерной форме представлено на рис. 7.3 и 7.4 для некоторых значений параметров % и (О, характеризующих свойства трещиноватого пласта. На графике рис. 7.4, а четко выделяются три характерные области. Первая область соответствует ранней стадии добычи, когда жидкость добывается главным образом из трещин. Для этой области, характеризующейся малыми значениями аргумента функции Ei, используя аппроксимацию Ei{-х)=-у-\пх в уравнении (7.24), можно получить:

0,80908 + In/g-f In-V

(7.27)

т. е. прямую линию в координатах Р-log t.

Если вмещающей способностью трещиноватой системы можно пренебречь, т. е. если © = 0, то начало добычи характеризуется скачком давления, который отражает отсутствие возможности накопления жидкости в трещинах (рис. 7.3, а).