Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 [ 90 ] 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

ницаемости К определяется коэффициентом турбулентности р. Ниже приводятся наиболее поздние, фигурирующие в литературе [11, 12] зависимости:

Р = 13,65 • 10"/(10-«Л:)- (6.42)

Р = 7,22-1010/(10-=/), (6.43)

где р-в 1/м; К - в мкм.

С учетом пустотности (пористости) [11]

Р = 7,22- 10V( 10-«/Ф)•°* (6.44)

где Ф - в долях единицы.

Справедливость этих уравнений спорна, так как экспериментальные результаты были получены при высоких значениях пористости (пустотности) и малых значениях проницаемости, в то время как для трещиноватых пород характерны очень малые значения пустотности и очень большие значения проницаемости. Однако с большой долей осторожности в качестве ориентировочных зависимостей эти уравнения могут быть использованы для оценки проницаемости. В общем случае уравнения (6.42) и (6.43) могут быть рекомендованы для моделирования отдельной трещины, а уравнение (6.44) -для моделирования системы трещин.

б. Число Рейнольдса

Для разграничения ламинарного и турбулентного течений в отдельных трещинах весьма хорошие результаты дает использование выражения (6.28) при критическом числе Рейнольдса, приблизительно равном 600. Если же рассматривается течение в трещиноватом пласте, то можно по аналогии с пористой средой воспользоваться уравнением в общем виде, например уравнением (6.40), выражающим число Рейнольдса в зависимости от следующих параметров:

Re = /(p,p, v, K/v).

Эти уравнения, определяющие число Рейнольдса, были получены путем обработки экспериментальных данных. В 1953 г. Щелкачевым [13] было опубликовано уравнение, учитывающее пористость:

р, (6.45)

в долях единицы. В этом случае критическое число Рейнольдса RckpI. Выведенное позже Гарстмом [10] уравнение определяет число Рейнольдса как

Re =

(5- 10-3)

ф5,5

- (6.46)

(5-10-3pt> Vk) 20

в случае сложной системы трещин при наличии данных исследования скважин можно рассчитать критический расход жидкости и критическую скорость, когда зависимость Q от АР становится уже нелинейной. Критическая скорость определяется по критическому расходу жидкости, а значение проницаемости пласта находится из уравнения (6.47).

6.2. Стационарное течение однородных жидкостей через систему трещин к скважине

Из промыслового опыта известно, что при эксплуатации скважин, вскрывших трещиноватые пласты, достигаются очень высокие дебиты (до 5000-8000 м/сут) прн весьма незначительных перепадах давления. Дебиты или коэффициенты продуктивности непосредственно зависят от наличия или отсутствия трещин, от их размеров и распределения. Данные исследования скважин на приток в условиях установившегося режима при правильной их обработке позволяют характеризовать систему трещин.

С целью упрощения предлагаются модели трещиноватых систем, основанные на правильных геометрических построениях. Все модели в идеале образуются группой однородных матричных блоков, разделенных трещинами, которые обусловливают небольшое сопротивление трения течению жидкости по сравнению с сопротивлением трения при фильтрации в пористой среде. Если матричные блоки настолько малопроницаемы, что подвижная жидкость сосредоточена только в сети трещин, течение к скважине будет определяться законами течения через непористую трещиноватую породу. Однако те же самые динамические условия имеют место и при высокой пористости матрицы, содержащей подвижную жидкость, во всяком случае, когда течение в системе стабилизируется и скорость вытекания жидкости из матрицы (питающей трещины) становится квазистационарной.

Следовательно, можно утверждать, что в системе с двойной пустотностью при стабилизированном течении процесс фильтрации жидкости к скважине происходит фактически только через систему трещин, тогда как течение от каждого матричного блока сводится к стационарной подаче жидкости в окружающие трещины.

6.2.1. Моделирование трещиноватой системы

Трещинно-матричный блок обычно моделируется по упрощенным геометрическим схемам. Классические схемы основаны на исполь-

зовании чередующихся по вертикали пропластков (блоков) матрицы, разделенных горизонтальными трещинами, или прямоугольной системы матрич,ных блоков, аналогичных тем, которые использовались в моделях, параметры которых приведены в табл. 4.6.

6.2.1.1. Упрощенные модели с использованием прямоугольных матричных блоков

Упрощенная модель трещиноватого пласта предполагает систему прямоугольных непрерывных однородных трещин, ориентированных таким образом, что каждая трещина размещается по направлению одной из основных осей декартовой системы координат. При равной ширине трещин каждого направления и равномерном их размещении модель будет соответствовать изотропной системе. Однако, если вдоль каждой оси геометрические размеры блоков будут разными, это уже будет моделирование определенной степени анизотропии. Модель, схематизированная таким образом, определяется размерами блоков, нх ориентацией и распределением. По результатам изучения кернов и выхода пород на поверхность, а также гидродинамических исследований скважин можно рассчитать такие характеристики, как проницаемость и пустотность матрицы и системы трещин и др., по которым составляются корреляционные зависимости для построения различных упрощенных моделей трещиноватой системы.

а. Эквивалентная длина прямоугольных блоков

Если размеры блока по осям х, у, z соответствуют ах, Uy и Uz (рис. 6.4), то эквивалентная длина блока / может быть рассчитана из соотношения поверхность - объем для п комбинаций трещин: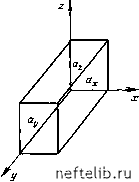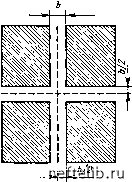

Рис. 6.4. Прямоугольный блок с плоскими трещи- Рис. 6.5. Поперечный раз-нами, ориентированными в системе осей х, у, г рез через смежные матричные блоки