Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 [ 45 ] 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

ям значений трещинной пустотности Фтр, в то время как сходства в изменении пористости матрицы Фм и трещинной пустотности Фтр не наблюдается.

4.2.3.3. связь трещинной пустотности Фтр с раскрытостью b и густотой Лг.тр трещин

если по результатам анализа керна известны средние значения раскрытости и густоты трещин, можно вычислить величину трещинной пустотности.

как указывалось в гл. 2, объемная густота трещин выражается формулой

г- TP -

где s - общая площадь поверхности трещин.

следовательно, чтобы выразить объем пустот, площадь следует умножить на величину раскрытости Ь:

-Объем пустот 1/28Ь

* Общий объем породы Vq

в случае изменения раскрытости трещин необходимо ввести ее среднее значение - Ь.

Пример. если средние значения Уг.тр и b равны соответственно 40 м/м (0,41/см) и 0,08 мм (8-10- см), трещинная пустотность будет равна

Фр = 8 X 10-3 X 0,4 = 3,2 X 10-» == 0,32%.

4.2.3.4. определение трещинной пустотности Фтр по шлифам

при оценке трещинной пустотности путем закачки в пустотное пространство образца легко фиксируемой (под микроскопом в шлифах) жидкости предполагается, что трещины будут заполняться более полно. следовательно, фиксируемые в шлифах трещины дают достаточно надежные значения трещинной пустотности. но эту трещинную пустотность нельзя рассматривать вместе с общей пус-тотностью образца, так как погрешности измерения общей пустотности стандартными методами оказываются одного порядка с величиной трещинной пустотности. причем неопределенность оценки возрастает, когда образец настолько мал, что его размер не превышает расстояния между двумя соседними трещинами. следовательно, измерение трещинной пустотности по шлифам является вполне приемлемым методом, особенно когда имеется достаточное число шлифов. исходя из параметра площадной густоты трещин, рассмотренного в гл. 2, величину трещинной пустотности можно выразить следующим уравнением:

ф Объем пустот Объем трещин

Общий объем породы Общий объем породы

Площадь трещин X Раскрытость трещин

Общий объем породы

В упрощенном случае, приведенном на рис. 4.5, видно, что истинная раскрытость b отличается от измеренной в горизонтальном плоском срезе Ьизм, поэтому

ф Ьизн cos ao/l/cos а b„3h ЬизнО

Для п параллельных трещин / (принадлежащих к системе трещин):

ф "&измД . д и

тр - „ - изм-г. тр "а

(4.6)

где а -протяженность единичной трещины; /тр -общая длина трещин.

В общем случае в каждом шлифе определяются величины бизн и /тр, а также площадь шлифа. Для п исследованных шлифов среднее значение Фтр будет равно

2 изм i тр г

Ф = тр

(4.7)

Точность определения пустотности повышается при увеличении числа разноориентированных шлифов.

4.2.3.5. Определение трещинной пустотности Фтр по геологическим данным о структуре

В гл. 1 было отмечено, что выведенное Муреем [4] уравнение (1.19) устанавливает зависимость между трещинной пустотностью и характеристиками структур. Это соотношение связывает толщину пласта Н и радиус кривизны структуры R с пустотностью в соответствии с предположением о том, что складкообразование может приводить к появлению трещин, перпендикулярных к напластованию. Тогда приблизительная величина пустотности

Рис. 4.5. Упрощенное изображение трещины в блоке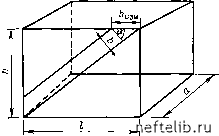

(4.8)

кривизна структуры (вторая

где Н - толщина пласта; dz/dx производная профиля структуры).

Так, для месторождения Антилоп-Сэниш-Пул (пример, рассмотренный в гл. 1) при кривизне (1,66-10-*ч-3,2) 10-" 1/м и Я/2 = 6 м

тр min

= 6Х 1,66Х 10-" = 0,1%; Фр„ах = 6x3 2x10-" = 0,2%.

4.2.3.6. Оценка трещинной пустотности Фтр

по данным испытания кернов при трехосном сжатии

Как указывалось в гл. 1, породы-коллекторы подвергаются воздействию нагрузки, обусловленной давлением вышележащих пород и поровым давлением Р, т. е. давлением; флюидов, насыщающих пустоты. Пластовые условия (давление, температура) так же, как и геологические факторы (образование разломов и складок), влияют на величину напряжений ст в породе-коллекторе. Поскольку в процессе истощения резервуара поровое давление Р будет уменьшаться, следует ожидать изменения величины напряжения, обусловленного давлением вышележащих пород о-Р.

Чтобы смоделировать пластовые условия, обычно в лаборатории проводят исследования при трехосном сжатии, регистрируя изменение величины пустности при действии результирующего напряжения, создаваемого весом перекрывающих пород [5]. Полученные результаты обычно изображают в координатах относительной пустотности ((Ф-Фо)/Фо и давления (о-Р). Как правило, результаты опытов показывают значительное изменение относительной пустотности при низких значениях ст-Р и наоборот (рис. 4.6).

Учитывая, что правая часть кривой (рис. 4.6) соответствует условиям, при которых изменение относительной пустотности обусловлено только трещинными пустотами, можно оценить трещинную пустотность, экстраполируя прямую до СТ-Р = 0.

На рис. 4.6 приведены результаты исследования трещиноватого известняка формации Кортеней (Фо = 9,8%; До = 0,265 мкм), относительная трещинная пустотность которого, получающаяся при

экстраполяции прямого участка кривой (Ф - Фо)/Фо от ст-Р равна 2,5%. Так как ф -Фо = Фтр, то Фтр = 0,025 X 0,098 = 0,00245-= 0,245%.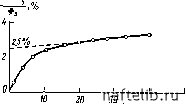

б-р. МПа

Рис. 4.6. График зависимости относительного изменения пустотности (Ф-Фо)/Фо от эффективного давления

(-Р) [5]