Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 [ 112 ] 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

функций Ei

Перепад давления APg

Номер уравнения

Ei -

Без изменения

~Ei I-

Ei -

-1-й,

itj \ ш(1-ш)

к -

(7.77)

In1,78

ш(1-<а)

In 1,78

2 со

(7.78)

in1.78

ш (I - ш)

In 1,78

Х<б

ДРб=-

- Ei

4<б ;

(7.79)

ш(1-со) X 1б)

In 1,78

i-co

ДРб +Ei

Х<б

ш(1-ш)

46 In 1,78

Х<б

I-©

(7.80)

ш(1-<о)

In 1,78

Х<б

Д/б =

1п1,26-

co(i-ш)

(7.81)

X \

ш(1-ш)

\ 4-ш

ДРб= -

/я2,24б/б-ЬЧ-

\ ш(1-ш)

- Ei

Х<б

(7.82)

X \

In 2,246 tb-Ei\ -

I-co

(7.83)

In 2,246 <б=- In<6+0,80908

(7.84)

случаи

In 1,78-

I-co

ДРб=-у

I \ X

-77 -In 1.78--tb

itaj 1-Ш

(7.85)

In 1,78

Хб I-co

ДЯб =

In 1,26 --

(7.86)

In 1,78

ш(1-<o)

In 1,78-

X<6

Ш(1-Ш)

ДЯб =

In 2,246 <б -f In-

(7.87)

Рис. 7.10. Кривая, иллюстрирующая падение давления при использовании модели Уоррена-Рута для случая R = oc. Цифры в скобках - номера уравнений

Последнее уравнение указывает на прямую взаимосвязь между относительной вместимостью со, падением давления АР и наклоном т прямого участка кривой (рис. 7.10).

Промежуточная стадия. Эта стадия соответствует переходному периоду между начальным моментом времени ta-.m, когда течение не подчиняется больше уравнению (7.78), и конечным моментом времени /к, когда течение подчиняется уравнению (7.84). Упрощенные уравнения (7.80) - (7.83), (7.85), (7.86), в основе которых лежат безразмерные параметры ie, Х.,ы, приведены в табл. 7.3.

Как видно, при определенном соотношении параметров X, <о и (б давление может оставаться постоянным во времени в течение периода установившегося режима в соответствии с уравнением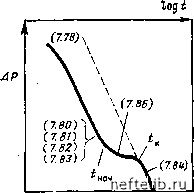

АР, =

In 1,26

1- (О

(7.86)

при использовании которого совместно с уравнением (7.78"), можно решить проблему одновременного расчета параметров К я а.

Конечная стадия. Падение давления на этой стадии (характеризующейся большими значениями to) выражается уравнением, аналогичным уравнению для пласта с межзерновой пористостью, так как и второй и третий члены в правой части уравнения (7.77) становятся пренебрежимо малыми по сравнению с первым членом (см. рис. 7.8). Это соответствует периоду, когда безразмерное время удовлетворяет условиям

и падение давления определяется уравнением (7.84) Д Рб = 4" " 2-2 и= -\nt6+ 0,80907,

- m log 2,246 9 (7.87)

или в размерном виде

тр =нач.пл - т log 2,246 t, = Р,„.„„ где m = l,15m.

Уравнение (7.84) выражает полустационарные условия фильтрации и описывает течение в трещинах, которое уже рассматривалось в гл. 6.

б. Анализ результатов

Ранняя и промежуточная стадии имеют место только при условии очень малых значений к что означает наличие существенного различия между физическими свойствами матрицы и трещин. Фактически, если к (й имеют высокие значения, аргументы второго и третьего членов правой части уравнения (7.77) велики даже при малых значениях tt и вторая и третья функции Ei становятся пренебрежимо малы по сравнению с первой функцией Ei в правой части этого уравнения. В таком случае поведение трещиноватого пласта на ранней стадии при неустановивщемся режиме фильтрации приближается к поведению непористого трещиноватого пласта, падение давления в котором выражается уравнением (7.84) (см.рис. 7.4, а для 0=0,1 и рис. 7.3, а для к<Ъ-\Ог).

И наоборот, если к а малы, обе стадии, ранняя и промежуточная, будут определяющими для процесса фильтрации в течение длительного периода, пока не будет достигнута асимптота (уравнение (7.84)) (см. рис. 7.4, а и 7.5). Для этого периода могут быть получены упрощенные формы уравнения (7.77): как показано в табл. 7.3, уравнения (7.78) - (7.87]Г. Многие уравнения такого рода контролируются зависимостью между © и h.

Характер падения давления, представленный на рис. 7.4, физически объясняется следующим образом. В промежуточной стадии после некоторого периода эксплуатации перепад давления, возникающий в сети трещин, способствует расщирению флюида в матрице, вследствие чего флюид покидает матрицу, начиная питать трещинную систему. Вторжение флюида матрицы в трещины снижает падение давления в трещинах подобно действию закачки флюида. И только позже, к концу этой фазы, матрица начнет регулировать питание трещин, обеспечивая подачу жидкости в соот-

Рис. 7.11. Иллюстрация аналогии между поведевнем жидкости в емкостях и в трещиноватом пласте.

j -большие резервуары (блоки матрицы); 5 -выход (скважииа); 3 - трубопровод (трещины)