Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 [ 115 ] 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Ф2 =

Ф, Ф

» 0,0117; :0,20;

= 3,87-10-* 1/МПа;

,р Ф2 = 0,0117;

1-Ф, S

= 0,285.

6. Параметр К получают по уравнению (7.95) как функцию ДРл =0,59 МПа (см. рис. 7.13 - при экстраполяции касательной в точке перегиба при 4= 1 илн =23 с):

>. = 0.56(1 - ш)е -3,6x10-6.

7. Параметр а находят нз уравнения (7.96): 1

= 1,5 1/м-

8. Эквивалентная длина блоков L определяется по уравнениям: для случая течения в трех направлениях L = У60/а=6,3 м; для случая течения в двух направлениях L= ]/ 32/а=4,6 м; для случая течения в одном направлении L=112/a=2,8 м.

7.2.4. Характер падения давления в случае R=Ro

Результаты замеров падения давления могут быть представлены в виде графика ДР-log / (рис. 7.14). Как и для случая Р = оо, ре-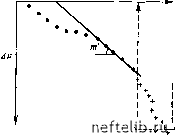

Зона!

\ Уравнения

Уравнение (7.W6)

ЗонаЗ равнение (,7.105)

Рис. 7.14. Кривая падения давления ири Рис. 7.15. Кривая падения давления

пуске скважины в трещиноватом пласте в скважине в трещиноватом пласте

для случая ограниченного (конечного) для случая ограниченного (конечно-

пласта. го) пласта.

конечная часть кривой p = f(fog t) соответ- безразмерное время: /5 - начальное,

ствует действительному положению о к - конечное

Стадия падения давления

10(1-т)

m(l-m)

За висимость ДР от

Наклон прямой

Очень малое

Малое

Среднее

Очень большое

Очень ()анияя

Ранняя

Промежуточная

Конечная

0-0,05 0,05 0,05-3 >3

1-0 О

(1-м)2

(1-м) VX

П р и м е ч а и и е. Наклон прямой равен т 1,74/r2,

Линейная Линейная Кривая Линейная

. 1-74

. 1.74

зультаты будут надежными до момента времени t-p, после которого линейная зависимость АР от log t уже не наблюдается.

На основании той же методики, которая используется прп i? = oo, можно рассчитать 6 по уравнению (7.89) и а по уравнению (7.76), а затем определить

Так как окончательный режим пласта устанавливается, когда изменяется наклон кривой давления при t = tF, то необходимо построить новый график по уравнению (7.70), которое можно записать в виде:

АР = Рнач.пл ~-Рскв= \h ~Fh\

(1 ш)2

1 -ехр

- (й) /

-R,, (7.103)

(7.103) (7.103")

Изменение АР от зависит от Ft (табл. 7.4). Поведение давления характеризуется наличием трех зон (рис. 7.15):

в зоне / (б малое и очень малое)

.(1 -a>)/J

/?б = 0,87 т (1п/?о -0,75).

АР= t,-

(7.104)

в зоне 3 (to очень большое)

l,74w

в зоне 2 - зоне перехода между /о.нач и б.к

АР; = [уравнение (7.105)] - [уравнение (7.104)]

(I -»)2 1,74

(7.105)

(7.106)

Величина Рб также может быть получена отсечением на оси ординат отрезка п использования уравнения (7.103) при 4=0. Наклон прямой линии зависимости ДР-/б определяется выражением \,7А тjR, где Ро известно и, следовательно, также известно т, по которому далее можно такй<е рассчитать К. Величина ш может быть определена по графику на рис. 7.14 с помощью уравнения (7.78") для случая R = oo как функция АР™ и т. Величина % находится по рис. 7.15 (по которому рассчитывается АРх.ш ), поскольку в зависимости, выраженной уравнением (7.106).

(1-<о)2 1,74/п

я, - единственный неизвестный параметр.

7.2.5. Динамика восстановления давления в случае Р = оо

7.2.5.1. Основные уравнения

Когда после некоторого периода эксплуатации скважину закрывают, наложение эффектов, действовавших в период эксплуатации и после ее прекращения, скажется на динамике восстановления давления (см. уравнение (7.32)).

Используя уравнения (7.77), с учетом времени Ato после закрытия скважины получим:

АР = т0,435 (~ Ei {--!-

+ Ei

I -(О

1 -О)

.(t,~M,)

+ Ei

4Д<б

(0(1 - ш)

j - Ei

(Р + АУ X

М(1 --ю)

(7.107)

В табл. 7.5 уравнение (7.107) представлено в различных упрощенных формах, в том числе при значительном изменении аргумента функции Ei.