Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 [ 126 ] 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Это уравнение может быть преобразовано для случая эквивалентного течения в изотропной пористой среде путем использования соотношения эквивалентности между геометрическими значениями и направленной проницаемостью. Упрощенное выражение такой эквивалентности

х.1х, = С\/к°, (8.42)

где С- эквивалентная константа.

Эквивалентность для трехкомпонентного соотношения

К=ук!щ[ (8.43)

и соответственно

хг = {кюк1ух,. (8.44)

Аналогично для двух компонентов

к = укчк2; (8.45)

x[ = {kvkt\; x, = ikvkiy\; Ciklktx (8.46)

8.3.2. Анизотропия и течение жидкости к скважине

8.3.2.1. Анизотропия в случае установившегося притока к скважине

а. Распределение давления

В первом упрощенном приближении можно рассматривать ортогональную систему координат х, у и z, где х и у - оси, соответствующие направлениям максимальной и минимальной осей эллипса проницаемости, а ось z совпадает с осью скважины.

Уравнение стационарного течения тогда имеет вид

Аналогичная процедура может быть использована для стабилизированного плоскорадиального течения, где эквивалентные параметры х\и л;2 будут связаны с эквива,яентной константой С (зависящей, например, от граничных условий):

Р {х, у) =--In г + С. (8.48)

2к Y Kj,Ky h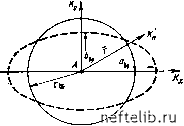

Рис. 8.6. Границы зоны дренирования скважиной в анизотропном и изотропном пластах. а - добывающая скважина

В цилиндрических координатах (рис. 8.6) распределение давления может быть записано в виде

Р{г) =

2IC VКхКу h

(8.49)

где г - радиус вектора, а К„ -проницаемость вдоль того же направления потока.

При постоянном давлении уравнение (8.49) будет уравнением эллипса, в котором отношение осей аэкв/экв пропорционально отношению Кх/Ку. Этот эллипс представляет собой линию изобар, а также линию, определяющую внешнюю и внутреннюю границы зоны дренирования скважины (рис. 8.6).

б. Эквивалентный радиус внешней границы зоны дренирования гдр

Граница анизотропного коллектора представляется в виде эллипса с осями йдр, бдр и может быть связана с изотропной радиальной границей Гщ, при помощи уравнения

= Кр + 6др)/2,

(8.50)

где физически соотношение осей пропорционально соотношению проницаемостей:

«др/6др = VX:7 (8.51)

Из этого следует, что оси эллиптической границы будут равны:

Адр = 2гдр 1/Х;/(/Д, + VKy); бдр = 2гдр VKJiVK+VTy).

(8.52)

Из определения эквивалентной длины

aj гда = С/Ук; и б;р/гдр = C/VTy. (8.53)

Размер эквивалентной радиальной границы притока может быть получен как функция данных по анизотропии:

«др + Р

4гяквС

2гэкбС

2 VKx+VKy VKx+VKy

(8.54)

в. Эквивалентный радиус внутренней границы зоны дренирования лскв

На основании того же определения эквивалентной длины, выражаемого уравнением (8.42), имеем

а«в/гс„в = С/УХ; &скв/>скв = G/T (8.55)

и далее выражения для параметров скважины

Гскв = (йскв + &скв)/2 = л,„«С {УТ + v1qi2 УЮГу, (8.56)

По аналогии для любого радиуса г в пределах области течения эквивалентный радиус будет равен

г = гС (/ЖГ + У%Г)/2 VKjTy. (8.56)

г. Эквивалентная радиальная скорость течения

Дебит скважины в пределах эквивалентной радиальной границы, исходя из уравнений (8.53) и (8.55), будет равен

2 1/:7/1 (Рдр-Яскв) 2иуХ1(Рдр-Рскв)

Q =---;-= - - (8.57)

(iD In- -

Гскв О+Кх/КуГ

2TiKh (Рдр - Рркв

г скв

t=4l C,/V(l + lx/.); K = VK,Ky. (8.59)

8.3.2.2. Анизотропия и интерференция скважин в условиях установившейся фильтрации

а. Вариант с двумя добывающими скважинами

В случаях двух скважин А и В, добывающих из одного и того же пласта, расположенных на расстоянии D друг от друга, классическое уравнение, описывающее интерференцию, имеет вид

27t уКхКу h (Рдр - Рскв)

глВ1пг;р7204в

где лдр, лскв и D - эквивалентные длины в однородном пласте, заменяющем реальный анизотропный пласт (рис. 8.7).