Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [ 16 ] 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

системы, обусловливающие высокую степень трещиноватости породы. Прерывистая связь между системами трещин в примерев соответствует невысокой степени трещиноватости. В примерах 2 и 3 одна из двух систем явно преобладает, причем в примере 3 связь между ними частично прерывистая. В этих случаях степень трещиноватости породы считается средней.

2.2.3.2. Блоки матрицы (вмещающая емкость)

Трещины, пересекающие породы-коллекторы в различных направлениях, ограничивают некоторые обособленные объемы, которые принято называть блоками матрицы. Каждый блок в такой системе гидродинамически не связан с соседними блоками. Правильнее считать, что каждый блок как бы обособлен внутри сети трещин. В действительности эти блоки контактируют в некоторых точках соприкосновения, но гидродинамические связи между ними остаются затрудненными.

Блоки матрицы характеризуются формой, объемом и высотой, а системы трещин - падением, простиранием и распределением трещин. Как правило, блоки матрицы имеют неправильную форму, но при решении задач эти формы стараются привести к простейшим геометрическим объемам (телам), таким, как кубы, вытянутые или плоские параллелепипеды.

Руланд [3] описывает различные формы блоков с помощью простейших геометрических фигур (табл. 2.1). Качественное описание формы в этом случае сводится к определению основных размеров каждого блока.

Пространственная ориентация блоков связана с тектоникой и с преобладанием одного вида напряжений над другим. В отношении моделей, представленных в табл. 2.1, можно отметить следующее:

а) блоки в виде колонн (табл. 2.1, строки 1, 2) - действие основных напряжений параллельно напластованию обусловило высокую степень трещиноватости;

б) плоские блоки (4, 5) - действие основных напряжений перпендикулярно к напластованию стало причиной высокой степени трещиноватости;

в) кубические блоки (3) образуются в тех случаях, когда действуют эквивалентные взаимно перпендикулярные напряжения.

Если известна ориентация трещин, можно установить структурно-тектонические условия образования трещин.

2.2.3.3. Густота трещин

Густота трещин выражает степень трещиноватости пород (коллектора) с помощью различных отношений. Густота трещин внутри объема называется объемной. Если рассматривается густота трещин относительно площади или длины, то она называется соответственно площадной или линейной.

Номер модели

Форма блоков

Геометрические модели блоков матрицы с размерами, см

100-10

а)< 5, у 1

Колонна

Малая колонна

Карандаш

Спичка

1-1- 1 5 2-

(l = L)

Большой параллепепи пед

Средний параллелепипед

Малый параллелепипед

fl = L =С)

Метровый куб

Дециметровый куб

Сантиметровый куб

2-5; (l = L)

Плита

Средняя плита

Малая плита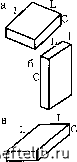

а) > 5; 1

Пластина

Средняя пластина

Малая пластина

б) 1; 4; S

Средняя пластина

Пластиночка

в) > 5; ; 2

Доска

Средняя доска

Линейка

Аналитически эти виды густоты трещин выражаются следующим образом. Объемная густота трещин Vr.rp - отношение общей площади трещин в блоке 5тр к объему матрицы (блока) У:

V..., = . (2.2)

Площадная густота трещин Лг.тр - отношение суммарной дли-

ны трещин тр = 2«~"тр к площади матрицы (общая пло-1

цдадь блока 8бл в сечении, перпендикулярном к потоку):

Л..р= = 4. (2.3)

-бл бл

Линейная густота трещин Lp.Tp - отношение числа трещин птр. секущих прямую линию (в направлении, перпендикулярном к потоку), к длине этой прямой линии Lбл•

г..р = . (2.4)

Линейную густоту называют также уровнем трещиноватости, частотой трещин или линейной частотой.

Примечание. Все три вида плотности трещин определяются длиной рассматриваемого элемента. Объемная плотность трещин - статический параметр (аналог пустотности), тогда как площадная и линейная плотности связаны с направлением движения жидкости.

а. Межтрещинный интервал

Интервал между трещинами - параметр, часто используемый вместо линейной густоты. Этот параметр выражает длину тела (элемента, блока) матрицы между двумя соседними трещинами и поэтому является обратной величиной линейной густоты:

е=-г-- (2.5)

г.тр

Часто эта величина выражается как среднее значение ё между максимальным и минимальным значениями Lr.Tp.

б. Густота трещин куба

В тех случаях, когда блок матрицы имеет форму куба со стороной а и при условии, что поток жидкости параллелен горизонтальным плоскостям (рис. 2.7), результаты исследований можно представить следующим образом. Объемная густота трещин:

площадь контакта поверхности трещины - матрица а; полная поверхность матрицы 6а-;