
 |
|
|
Главная Переработка нефти и газа б) трещинная проницаемость тр.влР/; (7.136) в) истинная проницаемость трещин тр=тр.вл/Фтр; (7.137) г) скин-эффект д) коэффициент заканчивания Сзи=4. (7.139) Такая аналогия имеет ограниченную применимость, и любой расчет параметров по этим уравнениям следует считать качественным, а не количественным. Пример расчета М 4 (Полларда) Скважина, пробуренная в трещиноватом пласте, эксплуатировалась в течение около 45000 с при установившемся дебите 491 мсут. Начальное статическое (пластовое) давление рпл=15,4 МПА; давление, зарегистрированное в момент остановки скважины, Рскв=14,9 МПа. Дополнительные данные: суммарная продуктивная толщина пласта /i=260 м; пустотность по геофизическим данным Ф = 26%; водонасыщеиность 5в.о=0,028, объемный коэффициент нефти Sh= 1,085; вязкость нефти 1Хн=1,2 мПа-с; сжимаемость трещин Стр= 1,17-103 1/МПа; сжимаемость матрицы См=0,54х x10-3 1/мПа; радиус скважины гскв= Ю см. Данные замеров давления и времени приведены в табл. 7.7. Чтобы проверить, соответствует ли модель Уоррена - Рута поведению пласта, можно воспользоваться традиционной зависимостью АР-logA (/o-f АО- Строится график (рис. 7.25) зависимости падения давления APi = Рпл-Рскв (табл. 7.7, графа 4) от At/{to+At) (графа 3). Полученный график не соответствует модели Уоррена - Рута, так как на нем отсутствуют обе параллельные прямые и переходный участок неустановившегося давления. Очевидно, переходный участок находится вблизи =1300 с, а первая прямая линия в интервале времени 1,5-10-2<A (/o-f А < <2,1-10-2 остается неопределенной вследствие влияния притока жидкости в скважину после ее закрытия. Наличие двух прямых участков кривой обусловлено уменьшением во времени наклона кривой с 0,298 МПа/цикл до 0,147 МПа/цикл. Так как условия модели Уоррена - Рута не выполняются, можно попытаться произвести расчет характеристик пласта по модели
Полларда. На рис. 7.26 показаны построения, на основе которых получаются приведенные ниже результаты. Наклон прямого участка кривой первой полученной зависимости log Робщ (см. табл. 7.7, графа 4) от времени At (графа 1) nti = 329 ООО с/цикл (МПа). .Этот наклон показывает время, необходимое для изменения восстанавливающегося давления на величину цикла. Экстраполяция кривой до At=0 дает Ср = 0,045 МПа. .АР, МПа 7,U7 МПа/цикл 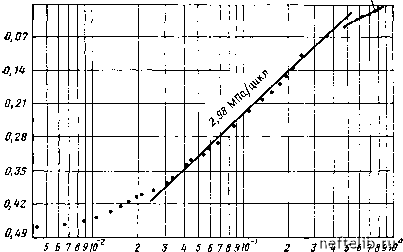 lotj At/(ig+Ai) Рис. 7.25. Кривая зависимости ДР - log A.il(ts + At) Все экстраполированные значения (графа 5) показывают паде-:ние давления в матрице: APm = APi. Вторая зависимость характеризует падение давления в трещинной системе (графа 6). Значения рассчитывались по формуле давления АР,р =АР2,з = АРобщ~Рм как функция времени М. Наклон прямого участка кривой выражает падение давления в трещинах: /Пз = 45 ООО с/цикл (МПа). Так как при А/=0 суммарное падение давления в трещинной системе определяется по уравнению f/p = Лр - Ср = 0,497 - 0,045 = 0,452 МПа, то суммарное падение давления в трещинах вокруг скважины выражается следующим образом: Sp=Up - D = 0,452 - 0,185 = 0,267 МПа. Интерпретация данных (модель Полларда): объем матрицы по уравнению (7.132) у = «!Ih 8,38-10 м г г 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 [ 120 ] 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |