Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 [ 131 ] 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

относительный упругий запас со и параметр x, характеризующий интенсивность перетока между блоками и трещинами:

X = (Хе-2==) e- (8.100)

где XeJ- соответствует кривой, с которой наилучшим образом совмещается кривая для исследуемого пласта.

Пример расчета. Результаты замера изменения давления во времени в скважине, добывающей нефть из трещиноватого пласта, представлены на двойной логарифмической диаграмме (см. рис. 8.16) в виде зависимости АР от t.

Остальные исходные данные: (7 = 572 мсут (6660 смс); рн = = 1,16 мПа-с; Вн=1,21; ft = 224 м; (ФУСобщ)трн-м = 3-Ю-" 1/МПа; гскв = 7,5 см.

Последовательность совмещения. Совмещая замеренные величины давления с кривой для Я,e- = 10~в и принимая Сбе25 = 10, по точке совмещения м получим (см. рис. 8.16):

Рб = 1,42 и АР =0,35 Мпа;

= 337 и А/= 1 ч.

Расчет основных параметров: из уравнения (8.95)

Ктр.ал = 66,5 мкм • м; из уравнения (8.96) С = 0,345 м/МПа; из уравнения (8.97) (Сб)тр+м = 152; из уравнения (8.98)

25 = 0,5 1п -= 1,15;

по уравнению (8.100) производим поверку значения x: X = 10-е е да ЮЛ

8.4.2. Эталонные кривые для исследования добывающей скважины, работающей при постоянном перепаде давления [6]

В этом случае падение дебита во времени анализируется по упрощенной модели Уоррена - Рута. Метод показывает, что для отно-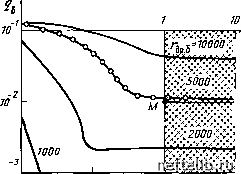

100 i,c\jj

\ n X X t X x,," ж "<

75ДмУсут

70°

Рис. 8.17. Типы кривых и данные падения давления в скважине для случая AP=const, со=10-з и >.= 10-

сительно больших пластов после первоначального снижения дебита наступает длительный период постоянного расхода. По совмещению определяются следующие данные:

тр.пл

9б /м

ФС = (ФУС)„ + (ФУС) - -22

(8.101) (8.102)

Пример расчета. На основании показателей добычи, используя диаграмму типа изображенной на рис. 8.17, где со=10- и Я,= 10-, по точке совмещения определяют:

7= 16,0 м/с для = 10-2;

t=l сут

для t. = к

Из уравнения (8.101)

Ртр.пл = 0,023 мкм из уравнения (8.102)

ФС = 1,66 • 10-* 1/МПа, откуда

Ф = 12,4 %.

Исходные данные, используемые в расчете, следующие: {гн= = 1,2 мПа-с; Вн=1,26; ft=120 м; АР=1,6 МПа; Гскв = 10 см, С«6,3-10- 1/МПа.

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ

А а В b

jfC -К ~

Q, q г S t

площадная густота трещин пьезопроводность объемный коэффициент раскрытость трещин эквивалентная константа, сжимаемость

расстояние между двумя скважинами

функция отнощения проницаемостей в анизотропном пласте

продуктивная толщина пласта

проницаемость анизотропная проницаемость

наклон кривой

давление

дебит

радиус

скин-эффект

время

скорость

V - объем е - угол

Ф - пустотность, пористость \ - межпоровый поток (J. - вязкость

ш - относительный упругий запас

ИНДЕКСЫ

X - больщая ось анизотропии у - малая ось анизотропии

1 -матрица

2 - трещина

СПИСОК ЛИТЕРАТУРЫ

1. Kazemi Н.. Seth М. S., and Thomas G. W., 1969. The Interpretation of Interference Tests in Naturally Fractured Reservoirs with Uniform Fracture Distribution, Soc. Pet. Eng. J., Dec.

2. Warren J. F. and Root P. J., 1963. The Behaviour of Naturally Fractured Reservoirs. Soc. Pet. Eng. J., Sept., p. 245-255.

3. Najurieta H. L., 1979. Interference and pulse testing in uniformly fractured reservoir. Paper presented at Las Vegas, Nevada, 541h Anual Fall muting. SPE 8283.

4. Elkins L. F. and Skov A. M., 1960. Determination of fracture orientation from pressure interference.

5. Bourdet D., Gringarten A. C, 1980. Determination of fissure volume and block size in fractured reservoir by type-curve analysis. Paper present at Fall meeting in Dallas, Texas.

6. Da Prat G., Cinco-Ley H., Ramey H. J., 1981. Decline curve analysis using type curves for twoporosity System. SPEJ, June, p. 354-362.