Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 [ 91 ] 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

I =--- при п = 3;

/ = - при п = 2; (6.48)

/ = при п = 1.

б. Эквивалентная пустотность схематизированной модели

Если блок окружают трещины с раскрытостью Ь, то только половина этой величины, т. е. bj2, относится к соответствующему блоку (рис. 6.5). Следовательно, пустотность прямоугольного блока равна

Ф.р = = + + -. (6.49)

ибл ах а-ч a-z

Если bx = by = b2 = b, то 1

Фтр = й

+ - +

(6.50)

и если ax=ay = a = a (в случае куба), то

Фр = 3й/а. (6.51)

в. Проницаемость трещин Ктр схематизированной модели

Как отмечалось в гл. 4, для отдельной трещины раскрытостью b и протяженностью / расход жидкости выражается произведением площади поперечного сечения потока S и его скорости v:

q =Sv = bl- - . (6.52) 12,0. L

Сравнение этого выражения с уравнением Дарси

bl - (6.53)

позволяет вывести зависимость между проницаемостью и гидравлическим сопротивлением трещины:

Ктр = ЬУ\2, (6.54)

где Ктр представляет собой истинную проницаемость трещины.

Для системы трещин (группы из п параллельных трещин) расход определяется по уравнению

q=.Sv = nbt , (6.55)

12fj. L

которое при сравнении с уравнением Дарси 284

к дя

q=S - (6.56)

дает следующее выражение эквивалентной проницаемости (как уже отмечалось в уравнении (4.27) и вытекает из уравнения (2.3)):

SK,.n==nbt- (6.57)

Атр.пл - •Р и IF

Другие зависимости для такого упрощенного моделирования приведены в табл. 4.1.

6.2.1.2. Основные параметры упрощенных моделей

Основные модели [14] изображены на рис. 4.20, а основные зависимости для них приведены в табл. 4.6. Прямые зависимости установлены между раскрытостью трещины Ь, интервалом между трещинами а, трещинной проницаемостью /Стр.пл и трещинной пустот-

ИиСТЫО Фтр.

Проницаемость /Стр.пл можно найти по результатам исследований скважин. Поскольку параметр Лг.тр часто определяется при обследовании керна и проведении каротажа, пустотность Фтр и раскрытость трещины b могут быть рассчитаны по уравнениям, представленным в табл. 6.1. Сами модели и направление течения показаны на рис. 6.6.

Например, при раскрытости трещины 0,1 мм в случае куба со сторонами 1 м из уравнений, представленных в табл. 4.6 и 6.1, получаются следующие значения пустотности и проницаемости для модели типа 6:

Ф,р = ЗЬ/а = 3- 10-V1 = 0,03%;

Стр.пл = Фтр/18 = (10-y-3.10-V18 = 0,17-10-8 см = = 0,17 мкм1

Использование упрощенных моделей, предложенных Рейсом [14], может привести к занижению пустотности, если она определяется по проницаемости, полученной по данным исследования скважин. Например, для случая ориентированного течения в системе трещин с неодинаковой раскрытостью эквивалентная проницаемость при последовательном соединении трещин определяется по величине среднего гармонического значения, на которую большое влияние оказывает величина наименьшей раскрытости трещин. Следовательно, пустотность, рассчитанная по этому значению, собственно говоря, не будет коррелироваться с истинной пустотностью. При использовании такой корреляции емкостная характеристика трещин будет занижена.

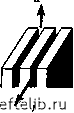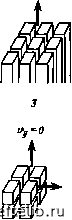Рис. 6.6. Основные варианты упрощенных моделей /-6 (см. табл. 6.1).

Стрелками показано направление фильтрации