Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 [ 117 ] 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Cl с,

Фтр = Ф.; ф„= •

Величина X может быть получена по уравнению (7.112) как функция APtr в течение переходного периода, замеренная в точке изгиба (см. рис. 7.16):

= Iog9(p-UA0+logi = log т 1 - со 1 - со

т откуда

х= -XQ""- (7.116)

Параметр поверхности контакта а рассчитывается так же, как и при падении давления:

Пример расчета № 2

После некоторого периода эксплуатацип скважина, рассмотренная в примере № 1, в момент времени /р=450 000 с была закрыта. По данным замеров давления была построена зависимость АР- -logA/(p+AO, приведенная на рис. 7.16.

По результатам восстановления давления определяются следующие параметры:

т=0,1134 МПа/цикл;

К„ = \,\Ъ - « 0,23 мкм

2т.к т

• loV-sS 1/с;

2,246<

-2,ЗДР / т

со=е " «3,1-10-

фС., = - » 1,22-10-5 1/МПа;

ФС,= ФгСг(1-м) 3 87.10-4 1/МПа; со

ф, =l да 0,017;

Тогда

Ф,р= 0,017;

Ф„ = --- » 0,29.

и параметр x из уравнения (7.116)

X = -1- joap,HeyCT/m 4 JQ.6

1,78 6 до

7.2.6. Динамика восстановления давления для случая R=Ro

В ограниченном пласте восстановление давления выражается уравнением (7.72), причем при решении методом суперпозиции член J?6 в уравнении (7.103) исчезнет.

Уравнение, определяющее восстановление давления, записывается в следующем виде:

ар -щИор + f,], (7.118)

Ч \ V ш(1 - со) j

Пользуясь критериями, принятыми в табл. 7.4, получим результаты, которые приведены в табл. 7.6. Как видно, ранняя и конечная стадии характеризуются постоянным падением давления (уравнения (7.120) и (7.121)), в то время как в промежуточной стадии (уравнение (7.118) давление зависит от времени:

. D 1,74т , 1,74 т (1 - о))2 i

Аг =--top -h •

Если в правой части уравнения (7.118) пренебречь первым членом, то log АР будет представлен следующим образом:

log APlog -bZi lill - 0,435 - At,. (7.122)

Rl X (1 -<o)co

Ha практике, если используется зависимость АР-log А (/б + -fA, то в результате строится диаграмма, аналогичная диаграмме для случая Р=оо, до момента достижения границы Ро, когда давление отклоняется от асимптоты (рис. 7.17).

Стадия падения давления

и>(1 -u))

Номер уравнения

Ранняя

Промежуточная

Конечная

0-0,05

0,05-30

30-ОС

(1-С0)2

Уравненне

(7.119)

1,74 m

(7.120) (7.118)

(7.121)

8 этом случае необходимо пересмотреть данные диаграммы logAP-tu, как показано на рис. 7.18, где три зоны определяются соответственно уравнениями (7.120), (7.118) и (7.121).

Используя график, приведенный на рпс. 7.17, можно рассчитать следующие параметры:

т - по наклону прямого участка;

со - по перепаду давления АР<о между параллельными прямыми линиями, определяя его значение по графику;

9 - по уравнению (7.115);

По рис. 7.18 определяется величина (1,74 т/Ро )ор, из которой можно найти значение Ро, и величина [0,435V(1-&))&)]- с/цикл - угол наклона прямой линии уравнения (7.118), где Л - единственный неизвестный параметр.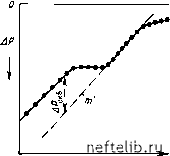

Log Ji/(i5+.4i)

Рис. 7.17. Кривая восстановления давления ДР -log Д</(<в4-Д0 в скважине в трещиноватом пласте для случая ограниченного (конечного) пласта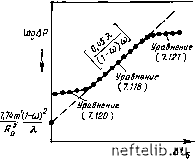

Рис. 7.18. Кривая восстановления давления log ДР-Дб в скважине в трещиноватом пласте для случая ограниченного (конечного) пласта