Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 [ 94 ] 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

55,5 -

рис. 6.16. кривая зависимости ap/q-Q

2. На основании уравнения &.P/Q=A + BQ и диаграммы на рис. 6.16 получаем:

Л =5,53-10-5 Mna/(cMVc);

в = 2,92-10-9 Mna/(cM=/cf.

3. Параметр А. Адаптация экспериментальных и теоретических данных. Уравнение (6.59) в случае Лтp.пл = Ь/12 и /1 = Ь примет вид

что показывает явную аналогию между уравнением Бейкера для трещиноватых пластов и уравнением для пористой среды.

Без учета скин-эффекта 25 на основании данных экспериментов Бейкера: Ь = 1 см, /•скв=0,076 м, /др = 1,524 м, цв«1 Па-с, вв = 1 получим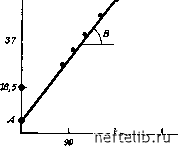

780 270

A = t\nJM.

; 5,5-10-5 МПа/(см»/с).

То же значение было получено по экспериментальным результатам на рис. 6.16, что свидетельствует о хорошем совпадении данных теоретических расчетов и экспериментальных результатов.

4. Параметр В. Адаптация экспериментальных и теоретических данных. Уравнение (6.60) при h = b принимает вид

рв5в

\ СКВ

др /

Подставив в это уравнение рв=1 г/см, вв=1, Ь = \ см, гскв = - 7,62 см, гдр =152,4 см, получим

5 = -3,10-10-8, МПа/(смс)1

Коэффициент турбулентности может быть рассчитан непосредственно по уравнениям (6.42) и (6.43) и результаты усреднены. Так как оба уравнения являются функциями проницаемости, параметр /С рассчитывается по уравнению (6.54):

£р = 1011 - - 10" = 8,4-10* мкм. 12 12

Далее из уравнения (6.42)

Pi = 3,24-10- 1/см; из уравнения (6.43)

р2 = 0,265 1/см.

Тогда

В, = 10-9 МПа/(см=/с)-;

Я, = 8,2-10-9 МПа/{ш/с)-;

B = (Bi + В)/2 = 4,6-10-" Mna/(cMVc).

Сравнивая среднее теоретическое значение S = 4,6-10- МПа/ /(см/с) с полученным экспериментально значением S = 2,92x XlO- МПа/(см/с), можно говорить о достаточно хорошем их совпадении.

5. Критическое число Рейнольдса Ке,ф. Критическое число Рейнольдса, выражаемое уравнением (6.28), является функцией критической скорости Укр:

Кбкр = рУкр2Ь/1-

При фильтрации воды плотностью рв= 1 г/см и вязкостью р = = 1 мПа-с при Ь = 0,101 см

Кбкр = 20у„р,

где Укр - в см/с.

Критическая скорость рассчитывается по величине максимального расхода Qmax, деленной на площадь фильтрации (боковой поверхности скважины 2лГс1;вЬ или 2лГсрЬ в середине модели). На основании рис. 6.15 при Ь = 0,101 см Qmax»1837 см/с (или 159 мсут). То же следует из условия Фтах=Л/В.

Тогда при Гср = 75 см*

ур = 1837/(6,28-75 0,101)«30 см/с

2-скв6

и, следовательно,

Re.p = 20ур = 20- 30 = 600.

Таким образом, можно сделать следующие выводы. Адаптация взаимосвязи теоретических и экспериментальных результатов определения параметров Л, S и Re,tp подтверждает справедливость выдвинутого предположения о том, что стандартное уравнение фильтрации в пористой среде может быть использовано при решении задачи радиального течения в отдельной трещине.

Рассмотренная выше задача ограничивалась случаем радиального течения в трещине, без учета толщины пласта (матрицы).Таким образом, результаты относятся к истинной проницаемости Ktp и раскрытости трещины b=-h.

Если задача решается с точки зрения трещинной пустотности Фгр, проницаемость /Стр.пл может быть отнесена к суммарной тол-

* в данном случае взят средний радиус модели, так как при лскв в трещине не будет наблюдаться турбулентности. - Прим. Ред.

щине продуктивного пласта, включающего трещины и матрицу. На основании уравнения (6.58):

/Стр.пл = A,.,{bV 12) = Ф,р (ЬУЩ = bVl2h,

что следует также из уравнения (6.66).

Если в данном примере густота трещин Лг.тр=1/м, т. е. 1/100 см,

/Стр.пл = 0,101=/(12-100) «8,4.10- см2 = 84 мкм1 6.2.3.2. Моделирование сети трещин

Задача моделирования геометрически неправильной сети трещин может быть решена по прямой с пористой средой или с помощью эмпирических уравнений, полученных из промысловых экспериментов.

с. Общая методика

Методика основана на использовании зависимости Q от ДР, полученной по данным испытании пласта, проводившихся на различных режимах при установившемся течении, и определенной густоты трещин Лгтр, следующей из результатов изучения трещиноватости или заданной модели. Порядок исследований представлен на рис. 6.17, где видна последовательность расчетов коэффициента продуктивности Р/ и коэффициента турбулентности р по параметрам А и В, приведенным на индикаторной диаграмме рис. 6.12. Величина К, полученная по параметру А пз уравнения (6.62), сопоставляется с величиной К, определенной по параметру В из уравнений (6.42) - (6.44). В результате расчетов находятся пустотность Фтр и проницаемость Ктр, которым для данной модели (см. рис. 6.6) соответствуют определенные значения Лг.тр, а п b (см. табл. 6.1). Система трещин, таким образом, представлена упрощенной схематизированной моделью.

б. Пример расчета

Задача № 1. Скважина исследовалась в условиях установившегося течения при разных дебитах Q и депрессиях ДР=Рдр-Рскв. Результаты исследований для четырех режимов:

Замеренные данные Расчет

Замер Q, м/сут ДР, МПа APQ, МПа/(мз/сут)

1 535 ..... 1,246 ........ 0,0023

2 1125 ..... 4,109 ........ 0,0036

3 1420 ..... 6,118 ........ 0,0043

4 1690 ..... 8,610 ........ 0,0051

Имеются следующие данные: p.ii=0,7 мПа-с; Вн=1,32; р„ = 0,8; /г= 160 м; Гскв= 10 см; Глр = 500 м.