Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 [ 95 ] 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

ЕЗ Ш ПП I

тип модели

Уравнение (6.63)

рис. 6.12

Т Уравнение (6.SO)

Уравнение (6.62)

Уравнения

(б.цг)

(б.цз)

проверка

Рис. 6.17. Пример последовательности расчета параметров по данным о притоке жидкостей

необходимо оценить пустотность, проницаемость и раскрытость трещины, задаваясь вначале моделью каземи, затем уоррена - рута, зная, что а= l/Lr.Tp= 100 см.

решение осуществляется следующим образом.

1. определение основных соотношений. на основании данных исследования скважин строится диаграмма (рис. 6.18), на которой представляются замеренные значения др в зависимости от q и рассчитанные значения отношения др/q в зависимости от q. экстраполируя график.зависимости др/q-q, получим:

л = 1/р/ « 8,16-10-5 мпа/(см/с)

и по углу наклона прямой линии

5= 1,77-10-8 мпа/(см/с)-.

на основании определения параметра А как величины, обратной коэффициенту продуктивности, при отсутствии турбулентности (т. е. при сокращении линейного закона):

р/ = \1А = 1/8,16- 10-S « 12000 (см=/с)/мпа.

по уравнению (6.41) общее уравнение течения имеет вид др = 8,16.10-5 q+ l,7710-8Ql

i3p, МПа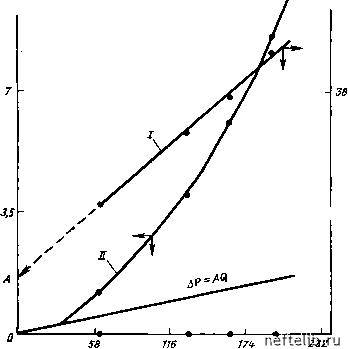

- 79,s

q, та CM/с

рис. 6.18. кривые зависимостей др/q-q (/) и лр-q (я), построенные по результатам дебитометрии

Расчет проницаемости ведется по уравнению (6.59):

0,0937 мкм1

V- ыв„ (1пЛдр/Лскв)

Коэффициент турбулентности р определяется из уравнения (6.60):

471:2 н-гсквв рнвн

или;

= 1,75-10" 1/см = 1,75-10l 1/м.

2. Вариант использования модели Каземи [16]. Для модели, приведенной на рис. 6.9, зависимость между различными параметрами соответствует зависимости варианта / на рис. 6.6 и в табл. 4.6 и 6.1.

Пустотность. Из табл. 6.1 Ф= (12/стр11л v4Vtp)== (12-0,0937х X 10-8-10-*)о-" = 0,04-10-4 = 0,0104%.

Аналогичный результат получен при использовании уравнения (6.63), где Р/=12000 cmVc МПа, а= l/lr.tp= ЮО см, Л = 0,12 1/см-(см. табл. 6.2).

Проницаемость Лтр.пл как функция р и Фтр рассчитывается по уравнению (6.44):

„ 10-3 / 7,22-10 \ 1/1.085

тр.пл=-- --- = 0,061- мкм.

тр.факт \ /

Величины /Стр.пл, определенные по параметрам В и А, различаются незначительно. Если разница между ними существенная, то это может свидетельствовать о влиянии скин-эффекта, которым пренебрегли в уравнении (6.62).

Истинная проницаемость трещины Ктр рассчитывается как

функция /Стр.пл и Фтр:

тр = /Стр.цд/Фтр = 0,0937/1,04-10-* = 900 мкм.

Раскрытость трещины b находится из табл. 6.1 для модели / по величине /Стр.пл, рассчитанной по параметру А:

b = (12/Стр.„л/Фтр)° = (12-0,0937-10-«)°= 1,04-10- см

Число Рейнольдса

Линейное течение наблюдается до критического значения дебита Q л; 3680 см/с. Критическая скорость в отдельной трещине при радиусе скважины Гскв равна

QhpBh -3680-1.32-

6,28.лс„вп6 6.28-10-160-1,04-10-2

где n=/ilr.Tp= 16 ООО -10-2= 160. Из уравнения (6.28)

Re„p = p2Kp/l = (0,8-2.0,0224-46,5)/(0.7-10-2) = 238.

3. Вариант использования модели Уоррена - Рута [17]. Пустотность рассчитывается следующим образом. Из модели 6 в табл. 6.1 следует:

Ф,р = (162 /Стр..л .тр )°= (162 • 0,0937 -10-«)°

Так как Лг.тр= (2/а), то

Фр = 3,92-10-* = 0,0392%.

Из уравнения (6.63) и табл. 6.2

ф (pj .нбн1пгдр/гснв4 г

тр~\ 2л/г г.трг.тр

0,33

ф 12000 ± 1,62 Г= 3,92-10-о/„.

6,28-16000 10*