Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 [ 123 ] 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

если

lO-« 10 , -

---1 ~ъ,

10-3 100

что приблизительно соответствует / = 5 с, когда этот член становится пренебрежимо малым; другой член

\ (0(1-<и) ;

Ei если

ш) г 10

что соответствует = 5000 с, когда этот член становится равным 0~ Следует заметить, что исследования по интерференции скважин могут показать характеристики пласта с двойной пустотностью только в том случае, если все члены уравнения (8.5) продолжают оставаться значимыми во время замеров в наблюдательной скважине. Из приведенного выше примера следует, что уравнение (8.5) сводится к уравнению (8.12) после = 5000 с.

Исходя из наблюдений, можно констатировать следующее. Характер двойной пустотности можно интерпретировать по имеющимся замерам, проведенным в наблюдательных скважинах,, только если а п X имеют небольшие значения. Такое условие соответствует средним значениям трещинной проницаемости и связано с значительным различием между проницаемостью матрицы и трещин.

Если а= 10", предел справедливости приведенных выше функций Ei уменьшается соответственно до 50 и 50000 с.

Если А,>10-5 и Лтр.пл =1 мкм то имеется большая вероятность того, что падение давления в наблюдательной скважине будет происходить аналогично падению давления в среде с одним видом пустотности - пористостью.

Если Ж10-" и /Стр.пл 0,1 мкм, наличие двойной пустотности может проявляться по замерам давления в наблюдательной скважине.

Оценка роли параметра X была проведена для постоянного значения (0=10-3 и двух значений га (1000 и 10000). Результаты, полученные при использовании уравнения (8.3), показаны на рис. 8.1. Так как асимптота отражает зависимость между давлением и Временем в условиях только пористой среды, все отклонения от прямой линии являются влиянием двойной пустотности. Из рис. 8.1 следует:

значение Я=10- (кривые 1 и 3) является нижним пределом значений X при расчете в случае двойной пустотности; фактически наблюдается небольшое различие проницаемости матрицы и трещин;

Рис. 8.1. Кривые зависимости Рк - te в наблюдательной скважине при различных значениях г о и X (m = = 10-3).

/-Гб = 1000. я,= 10-=; 2-Г6-1000. ?.= 10-=:

значение Я=10-*, соответствующее условиям значительного различия проницаемости матрицы и трещин, свидетельствует о существенных изменениях Рб2 в первый период замера падения давления в наблюдательной скважине;

влияние двойной пустотности проявляется более четко при меньших расстояниях между добывающей и наблюдательной скважинами (в случае 2 - гб = 1000 по сравнению со случаем 4-гг,= 10000).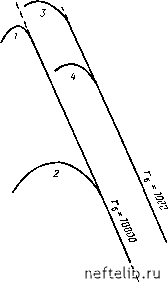

j i 1

ю ю ю w w ю" la" ю\

в. Размерное выражение падения давления На основании уравнений (8.3), (8.4) и (8.5)

Ар.пл=«

- Ei

- 0,25 - at

+ Ei

. 1-ш ,2 Ч ск

(1-ш) ,2 скв

(8.14).

- Ei

X а

log (2,246 а7/г-) +Ei \

1-ш

скв /

т = 1,15

?н ih дн 2r.h к.

тр.пл

(8.15) (8.16>

Справедливость приведенных уравнений следует из зависпмо-стей (8.6), (8.7) и (8.8).

8.2.1.2. Методика расчета

а. Использование основных уравнений

На основании регистрации давления в наблюдательной скважине может быть построена диаграмма зависимости падения давления от логарифма (рис. 8.2). Когда зависимость ЛР-log / изображается прямой линией, наклон прямой т даст падение давления за цикл времени, как и в случае пласта с межзерновой пустотностью.

Расчет трещинной проницаемости. На основании угла наклона т

/С=1,15. (8.17)

Расчет ньезопроводности а, При экстраполяции асимптоты до АРтр.п.я = 0 получим log 2,246 at/r-=0, что соответствует 2.246 а г/г2 = 1.

Определяя значения времени, как показано на рис. 8.2, получим а = [0,445 r/t]pf = 0,445 rVt. (8.18)

Расчет суммарной вмещающей способности ФС. На основании уравнения (8.4), используя значения а, рассчитанное ранее, получим

ФС = /С/ра. (8.19)

Расчет трещинной пустотности ФгФтр. По определению уравнения (8.4) трещинная пустотность определяется непосредственно:

ф.,=(ФС -ФА)/С2- (8.20)

Расчет соотношения пустотностей. со. Исходя из определения, данного в гл. 7,

о> = ф,С,/{Ф,С, + Ф,С,). (8.21)

Оценка обменной фильтрационной способности X. На основании рассмотренных выше пределов применимости уравнения (8.5) выражение для падения давления при ма-

Рис. 8.2. Кривая зависимости ДР - log t

log г в наблюдательной скважине