Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 [ 176 ] 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

11.2.2. Двухфазные модели 11.2.2.1. Теоретические основы

каземи [2, 3] разработал трехмерную модель двухфазного течения нефти и воды в системе скважин для трещиноватого коллектора.

уравнения течения получены в континуальном приближении, при котором перенос жидкости между трещиной и блоком представлен квазистационарной функцией источника - стока, пропорциональной разности потенциалов.

с учетом закона дарси и материального баланса в единичном объеме коллектора течение в трещинах описывается выражением

+ (с. + q - - div grad ф,,) +

Dj dt Bi dt \ inBi j

+ (t,,-t,,)-?i?(-xo)=0, (11.4)

где индекс i означает водяную (в) и нефтяную (н) фазы; индекс 1 относится к матрице, а 2 - к трещинам. обозначение s отражает геометрию элементов матрицы и, следовательно, влияет на обмен фазами между матрицей и трещинами. проводимость в этом случае выражается: для трещин

(11.5)

v \4Bi 1г для блоков матрицы

\ = [\S = V. (11.5)

потенциал ч,-, масса р,- и объемный коэффициент Вш- определяются следующими зависимостями:

b = PirPigZ\ pi=PoIi+q(i-)I;

(11.6)

b, = boi[i-q(i-)]-

где qi - дебит или расход на единичный объем ячейки хо-

с учетом тех же обозначений течение в блоке матрицы получим в виде

+ (q + q (ф,, - ф.)=0. (11.7)

Bi dt Bi dt (i-itSi

уравнения (11.4) и (11.7) записаны в полунеявной форме в виде конечных разностей и решаются с использованием методов гаусса - зейделя. элиминационный метод гаусса рекомендуется использовать при больших временных шагах, а один из методов sor, ad1p или s1p - при числе узлов, превышающем тысячу.

Модель можно легко использовать для расчета процессов пропитки с учетом гравитационных сил, фазовых проницаемостей и изменений коллекторских свойств.

11.2.2.2. Применение модели Каземи [2]

Модель Каземи применялась для расчетов пяти точечных элементов и залежи, дренируемой пятью скважинами. в модели трещиноватого коллектора, дренируемого пятью скважинами, принималось, что скважины расположены вдоль центральной оси X, угол падения пласта вдоль оси А составляет 5°. Каждый элемент сетки считался содержащим 25 блоков матрицы, что составляло 1625 матричных блоков во всем рассматриваемом объеме (рис. 11.3).

Параметры модели (Каземи [2]) следующие: /Ci = 1,0-10 мкм, 2 = 21 мкм2, ф, = 0,20, Ф2=0,10, 5 = 0,743-10-" м, СФ2 = сф,= = 0,21-10- МПа-, рв=1 мПа-с, рн=2,0 мПа-с, рв= 1,027 кг/м, р„=833 кг/мз, вв=1,0 при р = 0 МПа, бв = 0,976 при Р=55 МПа, в„=1,0 при Р = 0 МПа, вн = 0,92 при р = 55 МПа, рнач = 27,82МПа; размеры блока матрицы: 30,5x30,5x27,5 м; геометрия сетки: 13X5X1; Ал;=Аг/= 152,4 м; /i=0,3048 м; дебит добывающих скв. 1-5 составляет 159 м/сут; дебит внедряющейся в залежь воды на линии скв. 1, 3, 5 - 445 м/сут.

Результаты расчетов показаны в виде профилей насыщенности вдоль осевой линии X (рис. 11.4) и изменения водонефтяного фактора (виф) в скв. 1, 3, 4 и 5 во времени (рис. 11.5).

11.2.2.3. Моделирование капиллярной пропитки блока [3]

Моделирование процесса капиллярной пропитки трещиноватых образцов было проведено с помощью двухмерной, двухфазной математической модели. Геометрия блоков матрицы в модели допускалась как цилиндрической, так и прямоугольной, т. е. подобной форме искусственных образцов, описанных в гл. 9, разделе 9.5.2.3; результаты экспериментов приведены на рис. 9.65. Течение в трещинах описывалось уравнением

К.. %1 - (,3 - .з) + в5в I (X - хо) = ф,

(11.8)

где компоненты по Z заменялись на д

Уравнение течения в матрице имело вид

71Л]2в-к) = Ф1. (11.10)

где KixB = 0, а 540

заменялось на

т,Л,в-Ь.)- (11.11)

На рис. 11.6 приведены результаты одного из опытов в виде зависимости нефтеотдачи и обводненности продукции от объема нагнетаемой воды для образца песчаника Береа размером 2,54X Х7,62 см, первоначально насыщенного нефтью на 1007о- Вода закачивалась с относительно низким расходом- 1,07 см/ч. Из приведенного графика видно, что результаты расчетов хорошо согласуются с экспериментальными данными.

Основные исходные данные: Л = 4,76 см; L = 7,55 см; РУ= =6,62 смЗ; /(=97-10-3 мкм; Ф = 0,185; =1,07 см/ч; нефть -дизельное топливо; вода - раствор соли, 2 г/л; рн = 4,6 мПа-с; р,в = = 1,0 мПа-с; 5о.в=0. Экспериментально измеренные капиллярные

11.3

Рис. 11.3. Модель залежи: расположе-ние ячеек и вид ячейки трещиноватой среды [2]

Рис. 11.4. Распределение насыщенности вдоль массива добывающих скважин на различные периоды времени [2]: 1 - ъ трещинах; 2 -в матрице

Рис. 11.5. Изменение ВНФ во времени в добывающих скважинах как результат их расположения вдоль по восстанию пласта [2] 11.4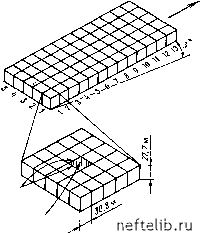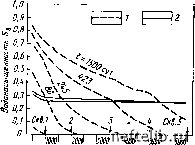

11.5

1,3 2,3 3,3 li,3 5,3 6,3 13 8,3 9,3 10,3 11,312,3 13,3 Расстояние вдоль массива продуктивных скважин, 10 м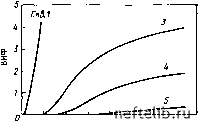

200 ш 600 800 1000 1200 МО Время, сут