Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 [ 135 ] 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

в этом случае безразмерное время определяется выражением

•"р-"--7-

и с учетом этого уравнение (9.20) можно записать в виде

б.гр.Н = (М - 1) Zg-fM + (1 - М) f 1 +

X Infl-f- -Zg). (9.22)

Как видно, существует заметное отличие уравнения (9.19) (вытеснение только за счет пропитки) от уравнения (9.22) (вытеснение за счет совокупного действия капиллярного и гидростатического давлений).

б.З. Случай преобладания гидростатического давления. Для случая вытеснения нефти только за счет гидростатического давления время вычисляют из уравнений (9.14) и (9.9) или путем исключения капиллярного давления из уравнения (9.22). В результате имеем

б.гр = (-l)26-ln(l-Z5). (9.23)

в. Замечания

Из теоретических результатов, полученных выше, особое внимание обратим на следующие.

в.1. Взаимосвязь / и Я. В обоих случаях, которые рассматривались, эта связь выражается зависимостью времени вытеснения от высоты блока Я:

при преобладании капиллярного давления tH (уравнение 9.18),

при преобладании гидростатического давления tH (уравнение 9.21).

В случае преобладающего вытеснения за счет капиллярного давления, что характерно для блоков малой высоты, существует параболическая зависимость времени от высоты блока.

в.2. Взаимосвязь t и Ze. Эта связь описывает поведение кривой нефтеотдачи во времени.

Когда преобладает капиллярное давление (уравнение 9.19), М играет важную роль:

/g.„«Zi/2, если М « 1; д.д « MZg, если М да 1.

При преобладании гидростатического давления (уравнение 9.23):

ts.rp « In (1 -Zg) - Zg, если М « 1;

б.гр«1п(1-Zr). еслиМ»1. (9.24)

Рис. 9.8. Перемещение фронта вытеснения в блоке, частично окруженном водой: ; - непроницаемая граница; 2 - вода; 3 - нефть в трещине; 4-нефть в матрице

Уравнения (9.24) совпадают с результатами экспериментов и различных теоретических работ [5], причем изменение нефтеотдачи во времени описывается выражением:

Zfi = 1 - еб-гр .

(9.24)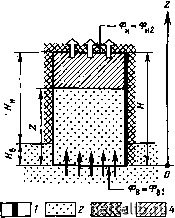

9.2.2.2. Нефтенасыщенный блок, частично окруженный водой

Нефтенасыщенный блок, частично погруженный в воду, моделирует случай медленного продвижения воды по трещине, причем граница раздела нефть - вода в блоке выше границы раздела нефть - вода в трещине. Упрощающим допущением служит предположение о том, что продвижение раздела в трещине пренебрежимо мало по сравнению с перемещением фронта в блоке, т. е. b = const (рис. 9.8).

В этом случае нефть из верхнего торца блока поступает в нефть, и потенциалы 0ei и 0 н2 (см. рис. 9.8) связаны с капиллярным давлением в трещине следующим выражением:

0В1 -0н2 = •Pк.тp + ёrWвДp• Пoдcтaнoвкa уравнения (9.25) в (9.8) дает:

- Р..

к.тр

-§(2-Яв)Др

(9.25)

(9.26)

{МН + (1 -M)Z]

Капиллярным давлением в трещине Рк.тр можно пренебречь, если его величина постоянна и много меньше капиллярного давления Рк в блоке. Уравнение (9.27) описывает именно этот случай:

Рк -Ь g (Яв -2) Др

(9.27)

[Л1я-Ь(1 -M)Z]

Одномерное вытеснение нефти только за счет капиллярной пропитки из блока с непроницаемыми боковыми поверхностями не зависит от положения ВНК в прилежащей вертикальной трещине, если кк>Нв-Z.

На расстоянии Z<H сила тяжести (гидростатическое давление) вносит свой вклад в вытеснение нефти. В случае Z>Hb гидростатическое давление замедляет процесс вытеснения. Однако когда боковые поверхности блока непроницаемы, вытеснение нефти из блока, полностью окруженного водой, может идти быстрее, чем из блока, частично погруженного в воду.

Эти выводы совпадают с результатами экспериментов Маттак-са [4], в которых определена критическая скорость подъема ВНК в трещине, выше которой скорость прироста нефтеотдачи зависит от скорости подъема ВНК и ниже которой скорость прироста нефтеотдачи остается постоянной.

9.2.3. Вытеснение нефти газом

Газ, поступающий в верхнюю часть блока, вытесняет нефть, которая выходит из нижнего торца в газонефтяную среду. Газ при этом считается несмачивающей фазой, сжимаемость его не учитывается.

9.2.3.1. Нефтенасыщенный блок, полностью окруженный газом

Нефтенасыщенный блок, целиком окруженный газом, показан на рис. 9.9. Начальное давление (давление газа) считается выше давления в блоке, и, следовательно, газ может входить в блок. Граничные условия, соответствующие этому случаю:

2 = я, 0r = 0ri;

Z = 0 0„=0„2, (9.28)

где Z=0+ - внутренняя точка границы блока.

Интегрируя уравнение (9.1) с учетом (9.28), получим: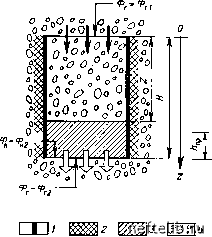

0rl~ ФгZ =

(9.29)

0Н2 =

(H-Z).

Складывая эти уравнения и заменяя 0rz-0hz = Рк-g(Я- - Z)Ap, получим:

Рис. 9.9. Перемещение фронта вытеснения в блоке, полностью окруженном газом:

/ - непроницаемая граница: 2-нефть в трещине; 3 - нефть в матрице; 4 - газ