Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 [ 108 ] 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

АР.. =

47г/Стр/1тр

El ~

(7.48)

где т)тр=Стр/ФтрцС - пьезопроводность трещиноватой среды.

Для малых значений аргумента экспоненциальной интегральной функции (Гскв/4т1<0,01) уравнение (7.48) можно аппроксимировать следующим образом:

-- (7.49)

АР =

На ранней стадии добычи падение давления является линейной функцией логарифма времени.

Когда жидкость добывается из трещин и падает давление, то жидкость из блоков будет перетекать в трещины. Считается, что жидкость, которая вытекает через площадь поперечного сечения Ли блоков матрицы, распределяется по половине трещины, где ее количество приблизительно равно Ам/1тр/2. Де Сваан получил решение уравнения (7.42) с асимптотическими значениями уравнений (7.43) и (7.44), аналогичное (7.49), но с модифицированной пьезо-лроводностью.

Для модели из плит:

7J= 1

тр.пл

тр • пл

для модели из сфер:

2 К«

тр.пл

3 /Стр h

тр.пл

(7.50)

(7.51)

где Гсф - радиус сферы.

Следовательно, при больших значениях времени зависимость между давлением и логарифмом времени опять становится линейной.

Графики зависимости Р-log / на ранних стадиях добычи и при больших значениях времени будут представлены двумя параллельными линиями, так же, как у Уоррена и Рута [1].

Решение де Сваана [5] не дает новых сведений о процессе течения жидкости в трещиноватых пластах и представляет только часть решения Уоррена - Рута, причем не вносит никакой простоты.

Как показал Каземи [4], квазистационарное состояние течения из блоков матрицы в трещины наступает очень быстро, и функция источника, пропорциональная перепаду давления в блоке и трещине, является удовлетворительной. Поэтому трудно сказать, имеет ли преимущество решение функции источника с использованием правильной геометрии блока по сравнению с решением Баренблатта.

7.1.3.4. Решение Наджуриета [6]

Наджуриет рассматривал общие выражения уравнений (7.45) и (7.46) и получил решение, справедливое также и для переходного периода течения.

Используя преобразование Лапласа в уравнении (7.42) с членом-источником, полученным из уравнения (7.45) или (7.46),Наджуриет получил

дтр =

y-(S) Ко

•1(S)

•S I г скв

(S) ;

(7.52)

где т) зависит от рассматриваемой модели блоков. Для модели из сфер:

niS)

4аг1

i/- coth f А ±

для модели из плит:

i(S)

tanh

(7.53)

(7.54)

Как видно, общее решение Наджуриета (уравнение (7.52)) аналогично решению Уоррена - Рута, но с другим определением т](5), следующим из иного определения параметров.

Решение уравнения (7.52) путем приближенного обратного (инверсивного) преобразования Лапласа (метод Шарпери) будет следующим:

( 4r,t)

(7.55)

где т) - функция времени, также зависящая от рассматриваемой модели трещиноватого пласта. Для модели из плит:

7] =

Kaha

фслг + 1/-7 tanh у/j

(7.56)

для модели из сфер:

7j = -

К oh 2

(7.57)

где а = /11/4ут1ь у - константа Эйлера. 336

Рнс. 7.8. Графическое сравнение решений Уоррена - Рута (/), Каземи (2) н Наджуриета (3) [6]

Сопоставление этого решения с решением Уоррена - Рута и Каземи приводится на рис. 7.8.

7.1.4. Особая модель-модель Полларда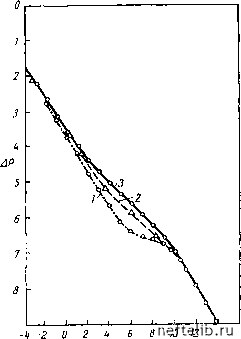

Теория Полларда [3] была разработана по данным анализа результатов кислотной обработки скважин в трещиноватых карбонатных коллекторах. Согласно этой теории, движение жидкости в пласте происходит в результате одновременного расширения жидкости, насыщающей пустоты обеих систем - матрицы и трещин. Это положение может быть выражено следующим образом:

/4 i,c

СтрФтр

= «(м--Ртр);

откуда получается дифференциальное уравнение

= 0,

А = ---я.

(7.58>

(7.59>

(7.60)-

(7.61>

СгрСмгрУм

Если уравнение (7.61) проинтегрировать при следующих граничных условиях:

для начальной стадии разработки при = 0 Рнач.тр=Рнач.м;

для более пбздней стадии при />0 уравнение материального баланса при расширении жидкости

(7.62)