Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 [ 105 ] 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Рис. 7.4. Графическая иллюстрация решения Уоррена-Рута [1] (уравнение (7.24)) для бесконечного пласта и некоторых конкретных значений параметров (О и Я.

Значения w: /-O.OOi, 2 - 0,01, 3-0,1. 4 ~ \; значения X: /-О, 2 -510-. 3 -S-IO-, 4- 5.10-9

Вторая область соответствует переходной стадии, на которой зависимость давления от времени в трещинах остается приблизительно постоянной, что соответствует ранним стадиям снабжения трещинной системы жидкостью из матричных блоков. Образование и продолжительность этой переходной области зависит как от О), так и от x.

Третья область соответствует большим значениям времени, когда достигается квазистационарное течение и весь пласт работает как эквивалентный однородный пласт. Поскольку проницаемость блоков низкая по сравнению с проницаемостью трещиноватой системы и ею можно пренебречь, то добыча из эквивалентного однородного пласта определяется проницаемостью трещин, а поведение пласта подобно тому, которое описывается в гл. 6.

б. Аналитические наблюдения

При больших значениях времени (7.24) стремятся к О, поэтому

обе £1-функции в уравнении

(0,80908 + In g = - In 2,25/g = 1,15 log 2,25g. (7.28)

В этом случае прямая линия будет параллельна линии, соответствующей начальной стадии добычи, и сдвинута по вертикали на 1п11/со. Наклон обеих линий равен -1,15/цикл. На рис. 7.3, б и 7.4, б показано отклонение прямых от асимптотического поведения, т. е.:

62 (i. б) - (0,80908 + In g) = Ei

,(1 - »)J

(7.29)

Разностные кривые, полученные по уравнению (7.29), пересекают ось Ад в точке

Agj= In 1/1/0). (7.30)

Точка пересечения с осью Рб2, касательной к разностной кривой в точке перегиба при б= 1, определится как

Аба = [-Т-1пХ/(1-(0)1/2.

(7.31)

Если Аб1 и Аб2 - известные величины, полученные в результате исследования скважины на приток, то могут быть определены параметры со и Я, характеризующие трещиноватый пласт с двумя видами пустотности.

7.1.2.2. Кривые восстановления давления в бесконечном пласте

Уравнение, описывающее восстановление давления, может быть непосредственно получено суперпозицией рещений уравнения (7.24) следующим образом:

А<б

+ Ei

Х(<б + А/б)

ш (1 -ш)

x (к + Мб)

1 -ш

+ Ei

1 - 0>

(7.32)

где /б - безразмерное время работы добывающей скважины; Д/д- безразмерное время с момента закрытия скважины.

Для больших значений времени добычи функция Ei, в которую входит параметр ta, будет быстрее стремиться к О, и поэтому асимптотическое решение уравнения (7.32) сводится к следующему:

хдб 1 - г хд<б р [ 1 -jj

f*62 =

to + Ate

- Ei

ш (1 - m)

(7.33)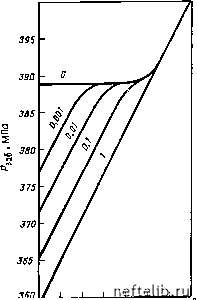

рнс. 7.5. типичные кривые восстановления давления [1] для бесконечного пласта.

я=5-10-= для всех случаев; 17=18,4 м/сут; t=2l сут; pgjg - забойное давление; шифр кривых-значения ш

а. Графическое решение

ю ю 10 73 10

t+Ai

Уравнения (7.32) и (7.33) имеют те же ограничения, что и уравнение (7.24), т. е. Д>100со для ?.<1 или Мб>ш1-1/к для со<1 и Я/б>3.

Вид уравнения (7.33) подобен виду уравнения (7.24), следовательно, и решения их подобны. На рис. 7.5 представлены типичные кривые восстановления давления при ,=const и ©, принимающем разные значения. При восстановлении давления могут наблюдаться те же три области пласта с разным поведением, какие имеют место и при снижении давления.

Ранние стадии восстановления давления иллюстрируются на графике участком прямой линии, соответствующим заполнению трещин жидкостью.

Вторая стадия (за прямой линией) характеризуется участком кривой, соответствующим квазипостоянному давлению во времени, в течение которого происходит массовый переток жидкости из трещин в блоки.

Третья стадия соответствует периоду, когда весь пласт ведет себя как однородный, что выражается на графике прямой линией, параллельной начальному участку.

Аналогичный анализ, проведенный при исследовании кривой падения давления, дает те же значения вертикального смещения двух прямых линий относительно друг друга в плоскости графика Рб2 - 1пА/(б + Дб), что и при исследовании кривой восстановления давления, равные Inll/co. Ограничение касательной в точке перегиба разностной кривой выражается зависимостью Д=Рб2- - п Аб/(б + Аб) от In б/(б+Аб). Это выражение получено для начального времени восстановления давления при Л=0, или

In А/ (/g-f A<s) = A.

Результат оказался тем же, что и для падения давления, т. е.: А = [-7 -1пХ/(1 - ш)]/2.