Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 [ 170 ] 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

пп-бп

(-/>вЯ,)

пл.бл

(10.35)

пл.бл

где индекс м соответствует модельным величинам, а индекс пл. бл- реальному блоку залежи.

Положим, что имеется п блоков, расположенных один над другим (рис. 10.29), и что капиллярная пропитка каждого t-ro блока начинается в момент времени „.нач, зависящий от скорости Vbhk, нефтеотдача как функция времени для всей серии блоков находится путем суммирования нефтеотдач из всех блоков от 1 до п.

Нефтеотдача при капиллярной пропитке выражается в процентах от конечной нефтеотдачи каждого блока (см. рис. 10.28) как функция времени:

где o.i-i - время начала капиллярной пропитки в блоке i. В случае постоянной скорости движения ВНК время

2 «бя

(10.36)

Конечная нефтеотдача для п блоков составит:

]?а1блФ(1-5,.нач)Ь

2 [1блФ(1-5,.,„)]( 1=1

(10.37)

или в случае, если размеры блоков равны,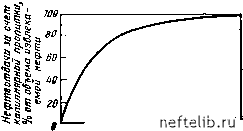

Время б ла(оаторных Время в плвстввых условиях

Рис. 10.28. Зависимость нефтеотдачи от времени для единичного блока матрицы

Рис. 10.29. Схема вытеснения нефти водой из вертикальной серии блоков

R.oH-Ri, (10.37)

где Ri - функция времени.

10.3.5.2. Аналитический метод

а. Модель Аронофского [8]

В вертикально расположенной серии блоков, отделенных трещинами, вытеснение нефти из каждого отдельного блока при подъеме ВНК в трещинах начинается в тот момент, когда вода вступает в контакт с блоком. Как показано в гл. 9, нефтеотдача единичного блока как функция времени может быть описана выражением

?=-?ко„ (1-еО, (10.38)

которое получено теоретически. Величина "к может в данном случае рассматриваться как параметр скорости вытеснения, обратный величине /кон=1Д, т. е. времени, необходимого для получения конечной нефтеотдачи /?кон.

В действительности, когда 1=1кон, произведение Wkoh-=1 и (1 - - 1/е)л;0,63.

Для серии вертикально расположенных блоков равных размеров (см. рис. 10.29) количество нефти в каждом блоке составит

азфЯд„ = аФ(1-5в.„„)Яб„ (10.39)

и соответственно для i-ro блока

Ni-=a<i,Zt, (10.40)

где Оэф - эффективное поперечное сечение потока в блоке.

Вытеснение нефти начинается в момент времени t>to4, когда вода вступит в контакт с i-м блоком, и, следовательно, количество извлеченной нефти из i-ro блока можно представить в виде

Лд,- = Л/,/?„о„(1-е-"), (10.41)

Если количество извлекаемой нефти представить в виде непрерывной функции уровня Z ВНК, уравнение (10.42) примет вид

Лд i = «эФ?ко„ f [l - е~ dz. (10.43)

Это же уравнение можно представить в виде зависимости нефтеотдачи от времени (так как Np=aHR):

R-jRoni~e-)dt. (10.44)

б. Модель Де-Сваана

Расход впитываемой воды на единицу протяженности трещины для одного блока

q = aRK,\t-., (10.45)

откуда для всего количества блоков берется интеграл от частной производной окружающей водонасыщенности:

<7;=«эф/?„он Г е "-dt. (10.46)

J dti

в. Другие упрощенные методы

Когда залежь в основном разбита субвертикальными трещинами, а горизонтальные трещины не прерывают течения жидкостей из блока в блок, блоки могут быть представлены идеализированной моделью, которая обсуждалась в гл. 4.

Поскольку в этом случае блоки удлинены в вертикальном направлении, можно считать, что гравитационные силы будут играть главную роль в механизме вытеснения, т. е. дебит будет задаваться следующим выражением:

q = a а-!. (10.47)

При этом все блоки можно разделить на классы по их проницаемости и пористости. Каждому такому классу соответствует определенное содержание нефти, которая будет извлекаться с характерной для данного класса скоростью. С учетом удельного веса блоков данного класса и соответствующих ему Ф, 5в.нач, К можно рассчитать общий дебит как сумму дебитов каждого класса:

qAL \]а,К,, (10.48)