Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 [ 156 ] 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

D,S-

Характеритики

рант

Рис. 9.64. Графическое изображение \ ОС-характеристик и фронта для ,u6 = 2,5 (а), Цб=1 (б) и Цб = 0,6 (в). Шифр кривых - значения водонасыщенности Sb2 в начальный .момент.

/ - скачок насыщенности по Балки-Леверет-ту для однородной пористой среды со свойствами, эквивалентными свойствам отдельных блоков; 2 - начальный фронт вытеснения

(52-0,72;

»0,1)

Рис. 9.65. Распределение водонасыщенности S„, (;) н Sb2 (2) в трещиновато-пористой среде для Цб=1,25 [19]. Шифр кривых - 0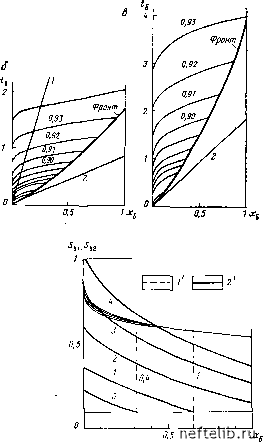

на то что в численных экспериментах использовались синтетические данные, сама модель и полученные результаты позволяют лучше понять с качественной точки зрения поведение трещиноватых коллекторов в процессе их разработки.

Решение типа Бакли - Леверетта для процесса вытеснения нефти водой (при постоянной скорости заводнения) из однородных коллекторов было совершенно неожиданно получено при решении приведенных выше уравнений, учитывающих блоковое строение коллектора, так как в этом случае система трещин играла роль проводящих путей, а блоки - роль зерен породы.

ОСНОВНЫЕ ОБОЗН.ЧЕНИЯ

А, В ~ константы

а - центробежное ускорение CGR - капиллярно-гравитационное отношение

CR - вертикальная составляющая .матрично-трещинной анизотропии по проницаемости d - диаметр пор f -: символ функции G - гравитационное давление

g - ускорение свободного падения

Н, h - высота

J - функция Леверетта К - абсолютная проницаемость L, I - длина

Л - число оборотов Р - давление R - нефтеотдача S - насыщенность S - коэффициент Sf - форм-фактор (фактор геометрической формы блока) t - время

<б - безразмерное время V - скорость

Z - конечное расстояние вдоль оси z

Z - текущее значение координаты вдоль оси Z 2б - безразмерное расстояние, эквивалентное нефтеотдаче

a, Р - обозначение уравнения

b, Ь. -, разность

Ф - пористость .(пустотность) Ф - потенциал X - удельный вес (а - вязкость

л •- безразмерный параметр р - плотность 2 - знак суммы

о - межфазное натяжение в - угол

ИНДЕКС Ы

б - безразмерный бл - блок в - вода в. св - вода связанная вн - вода-нефть выт - вытеснение г - газ гр - гравитационный 3 - залежь к - капиллярный кр - критический кон - конечный мод - модель, модельный

н.г - нефть-газ несм - несмачивающий н. о - остаточная нефть о. см - относительный смачивающей фазы о. и - относительная для нефти о. в -. относительная для воды о. г .- относительная для газа общ - общая пр - прорыв тр - трещина ф - фронт

оо - за бесконечно больщой промежуток времени

СПИСОК ЛИТЕРАТУРЫ

1. Muskat М.. 1949. Physical principles of oil production. McGraw-Hill Book Co., Inc., New York.

2. Blrks Т., 1955. A theoretical investigation into the recovery of oil from fissured limestone formations by water drive and gas-cap drive. Proc, Fourht World Petroleum Congress, Section П/F, Paper 2.

3. Leverett M. C, 1940. Capillary behaviour in porous solids. Trans. AIME, p. 152-159.

4. Mattax C. C. and Kyte J. R., 1972. Imbibition oil recovery from fractured water drive reservoir. Soc. Pet. Eng. J. (June), p. 177-184, Trans. AIME, vol. 225.

5. Aronofsliy J. S., Masse L. and Natanson S. G., 1958. A model for the mechanism of oil recovery from the porous matrix due to water invasion in fractured reservoirs. Trans. AIME, vol. 213, p. 17.

6. Boskerman A. A., Zheltov Y. P. and Kocheshkov A. A., 1964. Motion of immiscible liquids in a cracked porous medium. Soviet Physics Doklade (Oct.), vol. 9, No. 4, p. 285.

7. Kyte I. R.. 1970. A centrifuge method to predict matrix block recovery in fractured reservoirs. Soc. Pet. Eng. J. (June), p. 164-170.

8. Rapoport L. A., 1955. Scaling laws for use in field and operation of water-oil flow models. Trans. AIME, vol. 204, p. 143.

9. Lefebure du Prey E., 1978. Cravity and capillarity effects on the matrix imbibition, in fissured reservoirs. Soc. Pet. Eng. J. (June), p. 195-205,

10. Parsons R. W. and Chaney P. R., 1966. Imbibition model studies on water-wet carbonate rocks. Soc. Pet. Eng. J. (March), p. 26-34.

11. Iffly R; Rousselet D. C. and Vermculrn J. L.. 1972. Fundamental study of imbibition in fissured oil fields. Paper SPE 4102 presented at the SPE-AIME 47th Annual Fall Meeting, San Antonio, Tex.. Oct.

12. Blair P. M., 1960. Calculation of oil displacement by countercurrent water imbibition. Paper 1475-G presented at (he Fourth Biennial Secondary Recovery Symposium of SPE in Wichita Falls, Tex., May.

13. Graham I. W. and Richardson T. G., 1950. Theory and application of imbibition phenomena in recovery of oil. Trans., AIME, vol. 216, p. 377-385.

14. Kleppe J. and Morse R. A., 1974. Oil production from fractured reservoirs by water displacement. Paper SPE 5034 presented at the SPE-AIME 49th Annual Fall Technical Conference and Exhibition, Houston, Tex., Oct.

15. Kazemi H.. 1979. Numerical simulation of water imbibition in fractured cores. Soc. Pet. Eng. J. (June), p. 175-276.

16. De Swaan A., 1978. Theory of walerflooding in fractured reservoirs. Soc. Pet. Eng. J. (April), p. 117-226.

15. Kazemi H., 1979. Numerical simulation of water imbibition in fractured reservoir performance, based on physical Mobil experiments. 10th World Oil Congress, P. D. 10.

18. Barenblatt G. I., 1964. On the motion of a gas-liquid mixture in a porous fissured medium. Mekhanica 1 Mashinostroienie Izvestial Akademii Nauk USSR, No. 3, p. 47-50.

19. Braester C, 1972. Simultaneous flow of immiscible liquids through porous fissured media. Soc. Pet. Eng. J. (Aug.), p. 297-305.

20. Buckley S. E. and Leverett M. C, 1942. Mechanism of fluid displacement in sands. Trans., АШЕ, vol. 146, p. 107-116.

Глава 10

МЕХАНИЗМ ИЗВЛЕЧЕНИЯ НЕФТИ

ИЗ ТРЕЩИНОВАТЫХ ПОРОД-КОЛЛЕКТОРОВ

10.1, Введение

Инженеры-разработчики часто пытаются определить последующие параметры разработки залежей в трещиноватых коллекторах, исходя из истории их разработки, методами, принятыми для поровых коллекторов. Но, к сожалению, очень редко расчетные параметры, полученные по методикам, используемым для коллекторов порового типа, совпадают с реальными параметрами разработки трещинных коллекторов. Совпадение расчетных и фактических параметров может быть достигнуто модификацией основных исходных параметров вплоть до совершенно нереальных значений. Так, совпадение расчетных и фактических кривых может быть достигнуто искусственным завышением (в несколько раз) объема нефти в пласте. Невозможность достижения хорошего совпадения расчетных данных с фактическими показателями разработки при использовании методик, разработанных для поровых коллекторов применительно к трещинным, обусловлена особым специфическим механизмом нефтеизвлечения, присущим таким коллекторам.

Эти различия могут быть поняты при сравнительном анализе поведения порового пласта, параметры жидкостей и пород которого имеют тот же порядок величин, что и для трещиноватого пласта, но дополнительно обладающего широко развитой сетью тре-