Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 [ 129 ] 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

ф.р =

6. Различные случаи

1. Две взаимно ортогональные вертикальные системы трещин. Если bx=by, но Лг.трл;=7Лг.тр1/, густота трещин запишется в виде

4г.тр = Ai.tpX 4г.Тр!/.

Из уравнения (8.76)

г.тр X г.тр. v

12?. тр

в.тр X г.тр у

(8.81)

откуда

Фтр - .i4i,.Tp

г.тр X г.тр у

к„ Д.. in \/3

г.тр

PJ брнДн 1п"др/"скв «/i /Л.т-

(8.82)

г.тр ж "г.тр г/

Если bxby и Лг.трл:=г.тр!/=.4г.тр, трещинную пористость можно получить из преобразования уравнения (8.82):

Фтр = 2

PJ 6(ХнДп Inz-Bp/z-cKB 2

Tth

(8.83)

2. Три взаимно ортогональные системы трещин. Если bx=by = bz,

но Лг.тр;с.4г.тр!/т.4г.тр.г> то

Фтр - .i4i,.Tp

брнВн In /-др/Гскв

. (8.84)

V{\.rp X + г.тр у) (г.тр у + г.тр Z j

в случаях хаотичного расположения трещин или только одной горизонтальной системы трещин

4.Tp = (W2)Lr.Tp и соответственно

ф 1 р J 3,нДн 1пдр/скв

(8.85) (8.86)

8.3.3.3. Определение проницаемости и ориентации трещин по данным неустановившегося течения

Использование неустановившегося давления для случая определения анизотропной проницаемости с достаточной точностью возможно по методу Елкинса [4], который был применен при разработке месторождения Спраберри.

Приводимый ниже вариант метода для случая с двумя скважинами может быть далее распространен на большее число добывающих и наблюдательных скважин, расположенных на той же структуре.

а. Методика расчета

Рассмотрим добывающую скважину А и наблюдательную скважину В (рис. 8.12) в произвольно выбранной декартовой системе координат с центром 0. Будем использовать следующую методику расчета.

Для добывающей скважины А определяем наклон т из зависимости давления от логарифма времени, откуда получаем проницаемость

/( = 1.15

2nh т

Пьезопроводность может быть рассчитана по формуле

„/ К К

(8.87)

(8.88)

где Ф приближенно приравнивается к пористости матрицы Фь

Величины X-Хо и у-уо определяются для различных углов 0, как показано на рис. 8.12.

Для каждого угла 0 рассчитывается перепад давления по формуле

(х - х) + (у- Уо) 1

4а яям

АР = -т/2, 3Ei

(8.89)

где 4ам - замер времени на момент замера перепада давления в наблюдательной скважине; АРрасч - расчетный перепад давления из уравнения (8.89).

Отношение АРрасч/АРзам укажет наиболее вероятное значение угла 0, при котором АРрасч/АРзам» 1, как на рис. 8.13.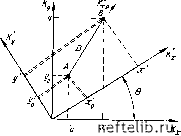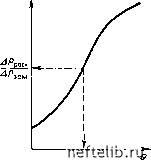

Рис. 8.12. Оценка угла 9 по наблюдениям и Рис. 8.13. Кривая зависимости расчетным данным о падении давления. (ДРрасч/ДРзам)-9

K".jp - проницаемость трещин по главной оси

Расстояние D остается неизменным, но его проекции изменяются с изменением угла Э.

Зная направление большой оси проницаемости Кп, можно оценить значения Кх и Ку, принимая, что для результирующего значения 9

У -У о

Решая это уравнение совместно с уравнением КхКу = К\

(8.90)

(8.91)

где К определяется из уравнения (8.87), можно оценить оба значения Кх и Ку

б. Обсуждение уравнения (8.89)

Падение давления в наблюдательной скважине в случае анизотропного трещиноватого пласта может быть описано следующим уравнением [4]:

<7fxS

2 2711/" КхКу h

(х~Хо)УК + {у-Уо)УКу j 4/ФС(х t

(8.93)

в котором, если х-Хо и у-г/о - значения проекции расстояния D на систему ортогональных осей Кх и Ку,

K, = K[D/{x~x,)] и Ку= KlD/{y-y,)].

(8.94)

Совместное решение уравнений (8.93) и (8.94) сводит выражение для падения давления в наблюдательной скважине к упрощенному уравнению (8.89).

в. Пример расчета

Скважины А - добывающая и 5 - наблюдательная исследуются в течение неустановившегося периода работы скважины А

(рис. 8.14). Необходимо найти анизотропию пласта на основании результатов определения зависимости давления от времени в скважинах А и В.

Известны следующие данные: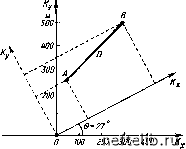

Рис. 8.14. Пример расчета анизотропии для скважин А (добывающая) и В (наблюдательная) в анизотропном пласте с осями анизотропии Кх и Ки