Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 [ 66 ] 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

трещинной системы в матрице с вероятностным коэффициентом взаимосвязи, равным 0,5, приведен на рис. 4.48, б.

Оценка остаточной нефтенасыщенности проводилась на модели Эрлиха [24J, состоящей из массива 12Х 12 каверн, сообщаемость которых выбиралась случайно в соответствии с заданным коэффициентом взаимосвязи /. При /, равном 0,5, число возможных местоположений трещин равно 312. Если одни трещины заполнены нефтью, а другие водой, то можно смоделировать процесс вытеснения. На рис. 4.49 показано изменение остаточной нефтенасыщенности для случаев вытеснения воды и газа в зависимости от коэффициента /. Результаты моделирования были сравнены с данными па керну. Совпадение результатов было удовлетворительным за исключением образцов породы с развитой вторичной пустотностью, в которых в случае несмешивающегося вытеснения наблюдались значительно более высокие значения остаточной нефтенасыщенности. Используя такие модели трещинно-матричных блоков, можно более обоснованно подойти к оценке процесса вытеснения.

г. Относительные проницаемости при фильтрации

в трещинно-матричных системах (теоретический подход)

Относительные проницаемости при фильтрации флюидов в трещинно-матричной или трещинно-матричной с микротрещинами системах могут изучаться по данным, полученным в лаборатории при исследовании обычными методами. Изучение с помощью этих методов оказывается более успешным, если в керне выделяется преобладающее направление трещин. К решению проблемы можно подойти, используя уже рассмотренные методы для случая неоднородных пород (составных слоистых пластов [24], каверн и трещин [31]). В результате могут быть построены кривые псевдоотносительной проницаемости.

Общие представления об относительных проницаемостях при фильтрации в трещиноватых породах были сформулированы Брис-тором [34]. В основном они сводились к следующему:

в трещиноватом пласте при существовании градиентов давления, возникающих в процессе капиллярной пропитки водой, между трещиной и матрицей будет происходить обмен жидкостями;

смачивающая фаза будет перетекать в матрицу, а иесмачивающая обратно из матрицы в трещины, во всяком случае в зонах, насыщенных соответственно водой и нефтью (рис. 4.50);

для такой модели относительные проницаемости становятся функцией степени насыщения трещин и пористой среды;

процесс рассматривается как непрерывное течение в обеих зонах - блоках матрицы и трещинах.

Схематичное представление таких кривых относительных проницаемостей приведено на рис. 4.51. Основываясь на предположении о непрерывности течения в блоках и трещинах, для таких случаев можно сделать следующие выводы.

Рис. 4.50. Схематизация процессов перетока смачивающей и несмачивающей фаз в матрице и трещинах [34].

Фазы: а-смачивающая; б - несмачивающая. / - матрица; 2 - трещина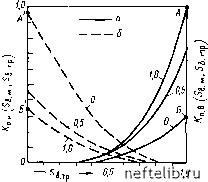

Рис. 4.51. Относительная проницаемость в трещинно-матричном элементе пласта-коллектора [34].

Кривые: а-ко,\ б - я- Шифр кривых - значения .S„ „

Форма кривых относительной проницаемости Ко.н и /Со.в будет изменяться в зависимости от водонасыщенности трещин 5в.тр (см. рис. 4.51).

Взаимосвязь между двумя относительными проницаемостями определяется выражениями

+ (1 - ) (1 -SU (1 -Sb.„)=] (1 -S,.J X

Дп.н =

->в. тр

jb. тр 1

(4.94) (4.95)

которые подобны уравнениям, предложенным Кори.

Основные данные с рис. 4.51 сведены в табл. 4.20.

Эти результаты можно проинтерпретировать следующим образом.

Точка А соответствует максимальной водонасыщенности матрицы и трещин: Sb.m=1; 5н.тр=1. Ни в матрице, ни в трещинах нефти нет - /Со.в = 1.

В точке Б Sb.„ = 0 и Sb.tp=1. Это означает, что матрица насыщена нефтью, а трещины - водой. Значения проницаемостей таковы:

o.bU = у

Др.в Is -

где К - абсолютная проницаемость трещинно-матричной системы; /Сф - фазовая проницаемость.

таблица 4.20

Применение результатов [35]. В случае идеализированной трещинно-матричной системы, состоящей из кубических блоков (рис. 4.52), значение проницаемости определяется по уравнению:

о. в. бл

для Sb.m = 0, 5з.тр= 1.

Исходя из рис. 4.20, по данным табл. 4.6 (для модели 6) получаем:

/Сф = /С™ = -:6Ф..=

6 а

Поскольку проницаемость трещинно-матричной системы описывается уравнением

тр. пл

= тр = +

о. в. бл-

1 + еКиа/Ь

(4.96)

что соответствует точке Б с насыщенностью 5в.м = 0 и 5в.тр=1.

Для обобщения этой модели был построен график зависимости Ко.и\б от Ь при различных значениях аКм (рис. 4.53). Из рис. 4.53 можно видеть, что при данных величине проницаемости матрицы и размере блока любое сокращение ширины трещины приводит К значительному уменьшению величины .Ло.в в точке Б. Другими словами, относительная проницаемость для воды велика в больших трещинах и имеет малое значение в очень тонких трещинах.