Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 [ 175 ] 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

бы функции источник - сток, функции переноса блок - трещина были определены apriori при лабораторных исследованиях на кернах либо с использованием математических моделей единичных блоков, или из анализа разработки конкретных залежей и вводились в ЭВМ как исходные данные.

Общим для всех моделей, описываемых здесь, является допущение о том, что течения и в трещинах и в блоках подчиняются закону Дарси.

II.2. Модели течений

11.2.1. Модель однофазного течения

Специальная идеализированная модель трещиноватой породы-коллектора, основанная на упрощающих допущениях Уоррена и Рута, была принята Каземи [1] при создании математической модели двумерного радиального течения. Модель представляет продуктивную скважину (рис. 11.1), разрабатывающую несколько горизонтальных участков пласта, разделенных трещинами так, что линии тока и в матрице, и в трещинах сходятся к скважине. Горизонтальные трещины представлены одной эквивалентной трещиной в качестве первого упрощения. Ниже приводятся другие упрощающие допущения, касающиеся характеристик коллектора и условий течения.

а. Матрица коллектора характеризуется высокой емкостью пустот и низкой проводимостью, в то время как трещины, напротив, характеризуются малой емкостью и высокой проводимостью.

б. Как результат предыдущего условия поток жидкости к стволу скважины обеспечивается в основном по трещинам.

в. Течение неустановившееся.

г. Залежь горизонтальная, матрица и трещины однородны и изотропны.

Основные уравнения: для матрицы

г дг \

дг ] dZ Ki df

для трещин с раскрытостью б

г дг [ дг Ь/2 [ dZ jz=b*/2 dt "

где б+ обозначает величину б на границе раздела трещина - блок, а потенциал равен

ф = р(0)

dP , „

(11.3)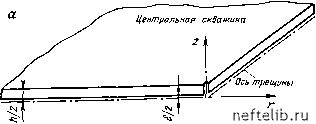

Ось ствола снватииы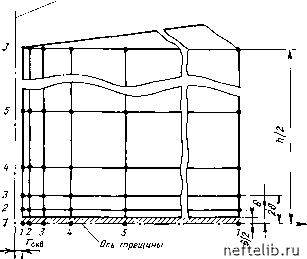

Рис. 11.1. Модель трещинного коллектора по Каземи [1]: а-скважина и коллектор; б - модель коллектора

При численном решении уравнения (11.3) Каземи пренебрегает гравитацией и заменяет Ч на Р. Граничные условия:

а) осесимметричного течения в блоках, которые соответствуют области применимости уравнения (11.1),

-<2 < - для Гскв < г < г„о„т;

б) осесимметричного течения в трещинах, которые соответствуют области применимости уравнения (11.2),

О < Z < - при Гскв < < конт;

я„мпа

21,5

25,5 -

w ю w 10 1

10 roo woo ч д U r~°"

27,5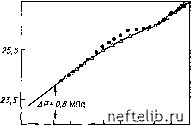

ю°т ro io w lo" lo lo r

Рис. 11.2. Сравнение результатов численного моделирования по Каземи и решения Уоррена и Рута [1]:

а -снижение давления; б - восстановление давления.

/ и 2 -модель Каземи для ограниченной залежи (фильтрация газа: / - только по трещинам, 2 - по трещинам и блокам); 3-модель Уоррена - Рута для бесконечной залежи

в) дебит трещин высотой б составляет аф 17" в

при О-

г) перенос жидкости к границе трещина - блок, осуществляющийся в вертикальном направлении.

- = 0; 8/2 <z<-; г = г,,,; дг 2

Модель применялась для анализа гидродинамических исследований скважин, и результаты расчетов процесса восстановления давления сравнивались с решениями Уоррена и Рута (рис. 11.2). Единственное различие между решениями Каземи и Уоррена - Рута состояло в появлении переходной зоны между начальной стадией добычи и асимптотой эквивалентного однородного коллектора. Это различие вызвано функцией переноса, принятой Каземи, в отличие от квазистационарной функции, принятой Уорреном и Рутом. Вся поверхность (блоков и трещин или только трещины) участвует в фильтрации. Это не влияет на результаты из-за резкого контраста между незначительной проводимостью блоков Kihi и очень высокой проводимостью трещин /Сг/г.