Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 [ 141 ] 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Bo8a

Рис. 9.28. Подъем воды в трещине [2]

г и Радиус пор, мкм

Рис. 9.27. Кумулятивные кривые распределения пор по размерам в матрице известняка [2]:

/-/<;-50-10-з мкм2, Ф-20%; 2 - К=1ЬЛй- мкм, Ф=20%; 3-К=Ъ-\й- мкм=, Ф=15%; 4-K=\-\f)- мкм2, Ф=15%

зультаты лабораторных исследований в натурные условия с целью более точного предсказания изменения величины текущей нефтеотдачи в процессе разработки залежи.

9.4.1. Концепция упрощенной модели 9.4.1.1. Капиллярная модель

Модель, разработанная Бирксом, представляет блок матрицы в виде пучка капилляров [2]. Число и радиусы капилляров определяются видом распределения пор по размерам (рис. 9.27). В единичной капиллярной трубке высотой Я (рис. 9.28) поднятие ВНК Z связано с перемещением ВНК Яв условиями равновесия между силами вязкого трения, гравитационными и капиллярными. Основное уравнение, определяющее это равновесие, можно записать в следующем виде:

HgpBr + 27Г/- cos е = 87гр, Z dZldt +

+ 87гг, (Я - Z) + rg [9bZ + Рн (Яв - Z)]. (9.46)

Если подъем ВНК в трещине происходит непрерывно {Hs = at), то уравнение, описывающее это движение, выглядит так:

8 [(Рв -lu)Z + РнЯ] dZ/dt + rg (р, - Рн) Z =

= arg (Рв - Рн) + 2/-а cos е. (9.47)

Если при этом вязкости нефти и воды равны (.хн = Лв), то уравнение можно записать следующим образом:

- + AZ = Bt+C, dt

(9.48)

где А, В я С - константы, определяемые из уравнения (9.47) и соответственно равные Л =/AY/(8гЯ); В = Аа; C=2/(7Cos 6/(8jiH). Решение уравнения (9.48) можно представить в виде:

Z = В (Л/ - 1)/Л2 + С/Л + De

(9.49)

Отдача каждой группы капилляров определяется выражением R = ZIHf (9.50)

которое показывает, что зависимость нефтеотдачи от времени имеет экспоненциальный характер.

Если ввести параметр извилистости для каждого цилиндрического капилляра, то уравнение (9.48) следует записать в ином виде:

dxldt + Ax = Bt + C\ (9.51)

А=А {LILf; В = В {LIL..f; С = С {LIL,,,f.

Пример. Средний радиус капилляров и их количество в % (табл. 9.2) приводятся Бирксом [2] для кривой, подобной кривой на рис. 9.27. Физические свойства жидкости: Лв = Лн=1 мПа-с, Pj, P„=0,4 г/смЗ, acose=10-2 Н/м2, Я=30,48 м, а = 7,3152 м/год.

Нефтеотдача за время подъема ВНК на высоту Z=L, которое составит i=30,48 м: 7,3152 мУгод=4,15 года, для каждой группы капилляров приведена в табл. 9.2.

Таблица 9.2

9.4.1.2. Модель поршневого вытеснения

а. Наклонный блок

Модель блока приведена на рис. 9.29, где показано поршневое перемещение фронта вытеснения, при котором водонасыщеиность на

Иещть

Уц. Воды в трещине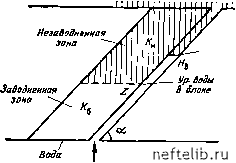

Рис. 9.29. Перемещение ВПК в блоке матрицы- и трещине [2]

фронте постоянна, а непосредственно за фронтом образуется остаточная нефть. Количество нефти, вытесненной из блока, составляет

Ф(5в-5з.„ач),

а скорость подъема воды в блоке матрицы описывается выражением, подобным уравнению (9.7):

dZ 1 Рк + Др (tf - g sin g) sin g

Д5вФ

Ab Ah

(9.53)

где ASb = Sb-5в.нач; Ар=рв-Ph.

Как видно, этот результат подобен решению уравнения (9.7) при а=90°.

Нефтеотдачу можно определить из выражения

2ФД Sb

= AS. = AS,Z,.

(9.54)

б. Вертикальный блок

Безразмерные уравнения, полученные в разделе 9.2.2, позволяют получить зависимость нефтеотдачи от времени.

Уравнения (9.19), (9.22) и (9.23) пригодны для общего случая. При преобладании гравитационных сил вычисление б.гр проводится с помощью уравнений (9.23) и (9.21). В случае преобладания капиллярных сил б.к рассчитывается из уравнений (9.19) и (9.18).

9.4.2. Зависимость нефтеотдачи от времени: общие положения и основные условия экспериментирования

Многочисленные теоретические и экспериментальные работы [4, 5, 6] посвящены исследованию зависимости скорости обмена воды и нефти в единичном блоке породы. На перемещение фронта вытеснения могут оказывать влияние как свойства матрицы и трещин, так и физические свойства жидкостей. В случаях очень высокой вертикальной проницаемости трещин фронт вытеснения в упрощенной модели принимается горизонтальным.

Различные авторы используют в своих экспериментальных работах модели, характеризующиеся различной геометрией блоков.