Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 [ 134 ] 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

а. Обсуждение уравнения (9.8)

Уравнение (9.8) выражает скорость как функцию разности капиллярного и гидростатического давлений, подвижности фаз и высоты Z фронта. Рассмотрим каждую из этих переменных.

a.l. Капиллярное и гидростатическое давления. Каждое из этих двух давлений в процессе вытеснения

Р„ -f G = Р« -f (Я - Z) gAp = /г„Ар -f (Я - Z) Ар

может оказаться доминирующим по сравнению с другим, и вытеснение нефти в этом случае будет определяться только одним из них.

Гидростатическое давление определяет процесс вытеснения при условий

G = (Я-Z)gAp»P„ = /r„gAp,

которое выполняется при наличии:

1) блоков большой высоты, когда (Я-Z)/Ik, а также в начальный момент вытеснения, когда Z невелико;

2) плохой смачиваемости матрицы, когда Рк ничтожно мало. В последнем случае уравнение (9.8) принимает вид:

-КЖ-. (9.9)

-" [МН+(\ -M)Z]

Капиллярное давление определяет процесс вытеснения нефти при условии

P, = h,gAp(H-Z)gAp.

Это возможно в случаях: блоков малых размеров Н<кк\

быстрого перемещения фронта вытеснения, так что ZaH, а

/1к>0.

При этом уравнение (9.8) можно переписать в следующем виде: и =--. (9.10)

а.2. Начальная скорость. Начальная скорость вытеснения соответствует моменту, когда Z=0, таким образом уравнения (9.9) и (9.10) принимают вид:

для гидростатического давления

« = «гр.„ач = - gAp = Ar. (9.11)

для капиллярного давления

и = «„.„ач = gAp = Ат. (9.12)

Отметим следующее:

начальная скорость вытеснения, определяемая гидростатическим давлением, игр.нач зависит только от физических свойств нефти и породы и не зависит от величины блока. Это уравнение получено Маскетом [1] для гидростатического вытеснения нефти из порового коллектора, а начальная скорость названа им гравитационной;

начальная скорость, определяемая капиллярными силами, «к.нач зависит ОТ размеров блока и изменяется от незначительных величин при больших Н до очень больших в случае малых Я. Это еще раз указывает на важную роль капиллярных сил яри вытеснении нефти из малых по величине блоков (малых Я).

а.З. Подвижность и скорость. Для выяснения роли отношения подвижностей м уравнение (9.8) лучше представить в виде

Кп йкА-г + (Я--г) А-г /913,

(х„ H-Z + ZIM

Заметим, что уравнения (9.11) и (9.12) получены для случая, когда отношение ZjM пренебрежимо мало, т. е. для больших значений подвижности, что характерно для высоковязких (тяжелых) нефтей. Интересно отметить, что в случае тяжелой нефти, насыщающей коллектор, характеризующийся большими блоками, скорость гидростатического подъема остается постоянной (уравнение 9.11) и независимой от относительного положения фронта вытеснения (Я-Z). Этот вывод находит подтверждение при разработке различных трещиноватых коллекторов, содержащих тяжелую нефть.

б. Перемещение фронта вытеснения во времени

Перемещение фронта воды во времени dzldt - истинная скорость перемещения фронта. Она связана со скоростью фильтрации через эффективную пустотность Ф классическим соотношением

u = Odzldt. (9.14)

6.1. Случай преобладания капиллярных сил. Подставляя выражение (9.10) в (9.14) и проводя интегрирование с учетом начальных условий / = 0 и 2 = 0, получим:

t= [MZ + {\~M)ZI2\. (9.15)

Капиллярное давление Рк как функцию насыщенности можно выразить с помощью функции Леверетта J {Sb) :

Р.={1{щ1уш)Л8в). (9.16)

При постоянном значении капиллярного давления /(5в) = 1. Подставляя (9.16) в (9.15), получим

t=--[MZ, + {\-M)Zll2l (9.17)

<f()VK о.в max

где Zu = ZIH и аналогично коэффициенту нефтеотдачи. 414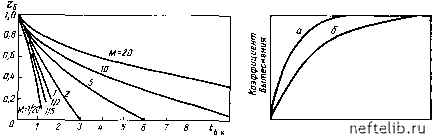

Рис. 9.6. Зависимость коэффициента вытеснения 2б от времени /б.к при различных отношениях подвижностей М [I]

Время

Рис. 9.7. Теоретическая (а) и экспериментальная (б) зависимости коэффициента вытеснения от времени

Уравнение (9.17) показывает, что время, необходимое для извлечения некоторой части нефти Ze при капиллярной пропитке, прямо пропорционально квадрату высоты блока и обратно пропорционально межфазному натяжению а, относительной проницаемости для воды Ко.в и квадратному корню из абсолютной проницаемости К-

Для определения безразмерного времени вытеснения при капиллярной пропитке воспользуемся выражением

а/(6)>/С/Ф

V-bM

(9.18)

которое можно записать в безразмерной форме:

t,., = MZ,-}-{\-M)Zll2. (9.19)

Зависимость доли извлекаемой нефти от безразмерного времени для различных отношений подвижностей была рассчитана Маскетом [1] (рис. 9.6).

Поскольку при расчетах предполагалось, что относительные проницаемости и капиллярное давление постоянны и не зависят от насыщенности, что не соответствует истине для реальной матрицы, оцениваемые значения времени занижены. Сравнение теоретических и экспериментальных кривых (рис. 9.7) может создать впечатление, что пустотность матрицы больше фактически измеренной.

6.2. Случай одновременного действия гидростатического и капиллярного давлений. Учет одновременного действия капиллярного и гидростатического давлений возможен путем интегрирования уравнений (9.8) и (9.14), что дает в результате

(М-1)2б-Гм + (1-М) fl +

x In 1

Др /

(9.20)