Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 [ 133 ] 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Рис. 9.3. Блок пористой матрицы с непроницаемой боковой поверхностью:

i и 2 - верхний и нижний торцы; 3 - непроницаемый слой

ны относительных проницаемостей и капиллярного давления являются функциями насыщенности. Решение этих уравнений возможно только при помощи численных методов. Для изучения влияния некоторых параметров на исследуемый процесс может быть использована упрощенная модель с плоской границей раздела между фазами. Аналитические решения таких задач составляют теоретическую часть главы.

При математическом моделировании принимаются следующие основные допущения.

1. Течение предполагается одномерным.

2. Капиллярное давление на межфазной границе постоянно.

3. Неснижаемая насыщенность смачивающей и остаточная насыщенность несмачивающей фазами принимаются постоянными и соответственно фазовые проницаемости неизменными.

Эти допущения использовал Маскет [1] при объяснении влияния отношения подвижностей на нефтеотдачу в условиях горизонтального вытеснения в коллекторах с постоянным давлением на границах.

4. Используемая процедура слегка отличается от метода Биркса [2], описывающего вытеснение нефти из блока трещиноватой породы.

5. Одномерным считается вытеснение из пористого блока, верхний и нижний торцы которого открыты для течения, а боковая поверхность непроницаема (рис. 9.3).

6. В окружающих блок трещинах распределение давления определяется гидростатикой, и поэтому потенциал ф =P + pgz является постоянной величиной.

7. Уравнения Дарси для смачивающей и несмачивающей жидкостей в блоке:

(9.1)

Мнем

8. Жидкости считаются несжимаемыми, и поэтому уравнения сохранения массы в каждой фазе можно записать в следующем виде:

duJdz = О, duJdz = О, (9.2)

откуда следует, что в течение рассматриваемого отрезка времени скорость течения каждой из фаз не изменяется. Поскольку на границах блока скорость течения обеих фаз постоянна, то с учетом уравнений (9.2) скорость течения должна быть постоянна в любом сечении потока, т. е. ucm = «hcm = w. При постоянной скорости уравнения (9.1) могут быть проинтегрированы.

9.2.2. Вытеснение нефти водой

Вода поступает в нижнюю часть блока, вытесняя нефть, которая выходит из верхнего торца блока в трещины, заполненные нефтью или водой. Вода - смачивающая, а нефть - несмачивающая фазы. Рассмотрим два случая, характеризующихся наличием или отсутствием воды на верхнем торце блока. Когда оба торца насыщены водой через соответствующие трещины, блоки считаются полностью окруженными водой.

9.2.2.1. Нефтенасыщенный блок, полностью окруженный водой

В случае, когда нефтенасыщенный блок полностью окружен водой (рис. 9.4), граничные условия записываются следующим образом:

2 = 0; 0в = 0в1.

где Н- обозначает высоту блока при ее отсчете внутри блока (Я+- высота блока, замеренная вне блока), а индексы 1 и 2 относятся соответственно к вытесняющей и вытесняемой фазам.

Решение уравнений (9.1) при заданных граничных условиях с учетом (9.3) дает:

(9.3)

(9.4)

0hz - 0н2 = «

-(Я-Z),

где Z - высота подъема фронта вытесняющей воды от нижнего торца (см. рис. 9.4).

Кроме того, заменив в уравнениях (9.4) 0Z выражением 0z = p-1-pgZ

Рис. 9.4. Перемещение фронта вытеснения в пористом блоке, полностью окруженном водой:

/ - непроницаемый слой; 2 - нефть; 3 - вода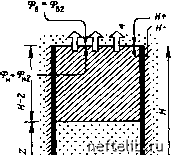

□И/ ШШ

Рис. 9.5. Изменение давления в капле во времени (по мере ее роста)

для воды и нефти, получим: 0в1 - 0Н2 + Рк - g2Ap =

+ (h-z)

(9.5)

где Ар = рв-рн.

Потенциал 0н2 на отметке Н- в блоке связан с потенциалом 0в2 в воде на верхнем торце блока (Я+) выражением

0Н2 =0в2 + Рк -ёДр>

(9.6)

где р - капиллярное давление на верхнем торце блока.

Для случая гидростатического равновесия, когда блок окружен водой и 0в2=0 в1, подставляя уравнение (9.6) в (9.5), получим

(9.7)

Z + -

(Я-2)

В экспериментах по капиллярной пропитке образцов, полностью погруженных в воду, было установлено, что вытесняемая нефть выделяется из породы в виде отдельных капелек на верхнем торце образца. Выделение нефти происходит при непрерывном увеличении размеров капли во времени до тех пор, пока выталкивающая сила не превысит капиллярные силы и не отделит каплю от матрицы. В действительности, капиллярное давление р изменяется во времени от некоторого максимума р = р, после чего капиллярное давление в блоке падает очень быстро с увеличением размера капли. Выделение нефти в виде капель на верхнем торце - прерывистый, пульсирующий процесс.

За цикл выделения одной капли время, в течение которого р равно Рк, относительно невелико (рис. 9.5) и Р очень быстро становится незначительным (уравнение 9.7) по сравнению с Рк- Поэтому можно записать:

Рк + §(Я--г)Ар fVfg(H-Z) Др

и =

(H-Z)

(9.8)

[МН+(\ -М) Z]

где Л1= (рн Сн)/(рв Св)-отношение подвижностей фаз - постоянная величина при принятых выше допущениях.