Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 [ 92 ] 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Рис. 6.7. Радиальное симметричное течение через сеть трещин, выражаемое по аналогии с течением через пористую среду.

h - продуктивная толщина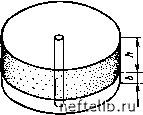

Рис. 6.8. Единичная трещина, моделирующая осесимметричное течение через систему трещин (модель Бей-кера)

ft - толщина слоя матрицы; 6 - раскрытость трещины

6.2.2. Моделирование радиального симметричного (осесимметричного) течения

Модель, схематизирующая течение флюида к скважине, предполагает радиальное симметричное течение в пласте от внешней границы зоны дренирования (боковая поверхность цилиндра Гдр) к забою скважины (боковая поверхность соосного цилиндра Гскв).

6.2.2.1. Типы моделей

а. Модель Бейкера [15]

В этой модели реальный пласт, образованный непроницаемыми матричными блоками, разделенными сетью трещин (рис. 6.7), представлен одним матричным блоком и одной трещиной (рис. 6.8). Равнозначность модели и реального пласта обусловливается одинаковой проводимостью модели и реального пласта.

б. Модель Каземи [16]

В этой модели сеть трещин трещиноватого пласта (рис. 6.7) заменяется равномерно размещенными горизонтальными матричными слоями, пространство между которыми моделирует трещины (рис. 6.9).

в. Модель Уоррена-Рута [17]

Трещины в этом случае образуют непрерывную и равномерную сеть, ориентированную параллельно основному направлению проницаемости (рис. 6.10). Предполагается, что раскрытость трещин постоянна. В случае анизотропной сети трещин или изменения проницаемости в определенном направлении должна быть смоделирована анизотропия. Расстояние между трещинами, определяемое их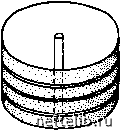

рис. 6.9. система параллельных трещин для моделирования осе-симметричного течения через систему трещин (модель каземи). Обозначения см. на рис. 6.8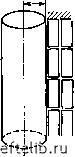

рис. 6.10. многоблоковая система для моделирования симметричного течения через систему трещин (модель уоррена-рута). а, - размеры блоков; скв - Радиус скважины

густотой, непосредственно влияет на величину трещинной пустотности и проницаемости. разрез, показанный на рис. 6.10, иллюстрирует модель, где блоками могут быть параллелепипеды, если йхйг, или кубы, если ах = аг.

г. Модель де Свата [18\

эта модель аналогична модели уоррена - рута, только матричные блоки имеют форму не параллелепипедов, а сфер. сферы укладываются в правильном прямоугольном пространстве. объем трещин представлен пространством между сферами (рис. 6. И), который далее коррелируется с значением пустотности.

6.2.2.2. Основные уравнения течения

можно предположить, что течение жидкости к скважине по системе трещин при хаотичном их распределении (см. рис. 6.7) происходит аналогично течению в пористой среде. Сеть трещин, состоящая из сообщающихся между собой каналов, характеризуется пустотностью, определяющей емкостные свойства системы, и проницаемостью, эквивалентной гидропроводности системы.

низкая пустотность и высокая проницаемость по аналогии с течением в пористой среде или по отдельным каналам будет обу-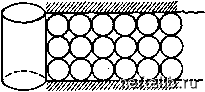

рис. 6.11. модель кубической упаковки сфер для моделирования симметричного течения через систему трещин (модель сваана)

Рис. 6.12. Индикаторная кривая Q-/(ДЯ), полученная методом установившихся отборов при осесимметричном течении в скважину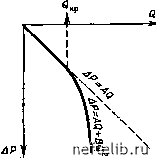

словливать линейную зависимость Q-ДР при низких дебитах жидкости и нелинейную - при значительньх. Остается справедливым классическое общее уравнение (6.41): AP=AQ + BQ.

Индикаторная диаграмма (рис. 6.12) показывает, что ламинарное течение AP=AQ имеет место до момента достижения критического значения Qkp. Если Q продолжает расти после достижения некоторой переходной зоны, то второй член в правой части уравнения (6.41) становится определяющим и течение почти полностью будет контролироваться законом турбулентного течения, выражаемым уравнением AP = BQ.

6.2.2.3. Расчет основных параметров упрощенных моделей трещиноватого пласта

Если предположить, ч,то сеть трещин характеризуется определенными значениями проницаемости К и пустотности Ф, то на основании уравнений (6.38) и (6.41) получим:

(1п/-др/гскв±2 5);

(6..59)

(6.60)

Если при исследовании скважин дебиты Q и перепады давления ДР замерены в условиях стационарного течения, то значения Л и В могут быть получены из уравнения (6.41), если его переписать в виде

(6.61)

и затем представлены графически (рис. 6.13). Прямолинейный участок полученного графика позволяет непосредственно определить значения параметра Л, равного ординате при Q = 0, и параметра В, равного углу наклона прямой линии.