Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 [ 162 ] 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Рис. 10.14. Многоэтажная структура взаимодействующих блоков

(Яг-2)Д-г-Р„

[МН - (\ -M)Z

(H~z)-h

(10.4)

Максимальная скорость дренирования, часто называемая гравитационной скоростью, определяется уравнением (9.38) (см. гл. 9), когда Рк=0 (что эквивалентно/гЯ), а Z = 0 (эквивалентно 2<Я), при этом

Q«p==Q„,ax =

(10.5)

Дополнительный расход из блока i-1 (см. рис. 10.14) через область смачивания обозначается Q, i пер i И может быть И большс, U меньше максимальной скорости дренирования блока Qmax.

Если Qi-i пер i<Qmax/, ВСЯ нефть, поступающая из верхнего блока, впитывается в блок l

Если Q(-inepi>Qmax/, некоторое количество нефти (избыток) течет по трещинам блока i.

Дополнительный расход может быть выражен следующим образом:

Qi-l пер i ~ лр + Qh36 г-1>

где Qnp чаще определяется по уравнению (10.5), чем по уравнению (10.4).

Скорость впитывания равна дополнительному расходу при условии, что дополнительный расход меньше максимальной скорости дренирования. Это описывается выражением

QaniiT i ~ Qi-i пер

если

Qi-l пер i Qmax i-

Избыточный расход равен количеству нефти, текущей по трещинам

Qn36 г ~ Qi-l пер i Qap i

причем это имеет место только, если

Qi-l ntp i Qniax г

в. Степень блок-блокового взаимодействия

Если степень взаимодействия выражать параметром а, то ему можно приписать следующие значения: полное взаимодействие соответствует а=1; частичное взаимодействие соответствует 0<а<1; отсутствие взаимодействия соответствует а=0.

Основываясь на этом, можно вывести соотношения между параметром а и расходом: а= 1 - соответствует Q(-inep(<Qmaxi;

а<1 - соответствует Q, i пер <>Qmax <

Другими словами, когда а=1, вся нефть, вытекающая из блока i-1, впитывается в блок i, если же а<1, часть вытекающей нефти вынуждена течь по трещинам, окружающим блок i. В случае а<1 часть вытесненной нефти, которая фильтруется вниз по трещинам, может вновь начать впитываться, причем остаток (не-впитавшаяся нефть) в точности равен избыточному расходу:

Qi-l пер i>Q max !•

При отсутствии взаимодействия с прилегающими блоками, если а=0, задача сводится к случаю единичного блока.

г. Экспериментальные наблюдения

Проведенные в лаборатории эксперименты с использованием двух блоков (см. рис. 10.12) позволили выявить следующее:

нефть из блока / движется через блок 2 вместо того, чтобы течь по его поверхности;

несмотря на то что область смачивания, через которую поступает нефть, мала, скорость впитывания часто бывает достаточно высокой;

пониженные скорости впитывания наблюдаются на плоских блоках, когда область смачивания располагается на одной из сторон блока;

скорость впитывания зависит от формы и размеров блока, а также от расположения точек, через которые поступает нефть, изотропности матрицы и наличия непроницаемых прослоев.

д. Поведение насыщенности при поступлении нефти в верхнюю поверхность блока в процессе гравитационного дренирования

В блок матрицы i поступает нефть с объемной скоростью Qnep и из него же оттекает благодаря гравитационному дренированию Qmax- При этом насыщенность блока остается постоянной, если обе скорости постоянны. Величина отношения Q = Qnep/Qmax определяет высоту капиллярного подъема и распределение в блоке насыщенности согласно уравнению

1 Q -\-

(10.6)

Q=D,D1 0,1 0,5 0,3 0 i 0,05 0,2 0,75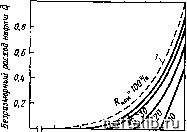

0,2 0,k 0,6 0,8 1,0 , Приведенная нефтенасыщенность S„

0,5 0,B 0,7 0,8 0,9 1,0 Приведенная нертенасыщенность sj

Рис. 10.16. Зависимость безразмерного расхода нефти Q от средней нефтенасыщенности S*H при различных величинах нефтеотдачи R„oH (1 - кривая относительной проницаемости для нефти) [2]

Рис. 10.15. Профиль нефтенасыщенности в блоке матрицы, когда нефть нз области смачивания фильтруется через блок [2]:

1 - кривая капиллярного давления; 2 - высота блока

которое по,?1учено из уравнения (10.3), причем dPjdS* взято с учетом уравнения Леверетта

Р=сУфШ (Sl). (10.7)

Профиль распределения насыщенности в блоке зависит от величины отношения Q, как это следует из приведенного расчета [2]. Причем относительная проницаемость принята в виде Ао-н = (н)» а величина конечной нефтеотдачи Р = 31,5%. Из рис. 10.15 видно, как изменяются стационарные профили нефтенасыщенности при изменении Q от О до 1.

При Q = 0 (что предполагает quep = 0) профиль насыщенности определяется кривой капиллярного давления (рис. 10.15).

Увеличение отношения Q от О до 1 приводит к возрастанию величин нефтенасыщенности S*, так как поступающая в блок нефть

компенсирует часть продуцируемой блоком нефти. При q=l нефтенасыщенность блока практически неизменна, что должно соответствовать отсутствию продукции, однако процессы дренирования осуществляются в каждом единичном блоке.

Как отмечалось, зона капиллярного подъема более обширна у нижней грани блоков н уменьшается с увеличением его высоты. Таким образом, вблизи верхнего торца блока S„ велико, особенно в зонах пониженной гидрофильности пород, и Ан достаточно велико, чтобы обеспечить внедрение нефти в матрицу. Средняя нефтенасыщенность блоков в зависимости от безразмерного расхода Q для заданных конечных значений нефтеотдачи приведена на рис. 10.16. Для значения кон=100%, соответствующего Рк = 0,