Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 [ 47 ] 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

Рис. 4.9. Радиальное течение по направлению к скважине. Модели: а - Каземи, б - Уоррена-Рута

тр. пл

Ql [1пгдр/гскв + S]

2nhAP

(4.19)

Связь общей проницаемости /Стр. пл, полученной по уравнению (4.19), с составляющими проницаемостями Км и Ктр будет зависеть главным образом от выбранной модели пласта-коллектора. Другими словами, идеализация трещинно-матричной системы по какой-либо модели будет в дальнейшем определять соотношение между /Стр.пл и Км, /Стр. На рис. 4.9 показаны идеализированные модели, обычно рассматриваемые в литературе:

а) модель Каземи [7] - образована чередующимися слоями матрицы и трещинами (рис. 4.9, а);

б) модель Уоррена -Рута [1] - образована блоками кубической формы, разделенными ортогональной сетью трещин (рис. 4.9,6).

В модели Каземи течение осуществляется по слоям с различной проницаемостью параллельно напластованию и

тр. Пл

= -м + тр = +

в модели Уоррена - Рута механизм установившегося притока флюида совершенно другой. Блоки матрицы постоянно подпитывают трещины, и флюид течет в направлении к призабойной зоне только через сеть трещин. Следовательно, в соответствии с уравнением (4.19)

тр. пл ~ тр-

Вывод. При испытании скважин в условиях установившегося притока получается одно значение проницаемости, которое может интерпретироваться по моделям Каземи или Уоррена - Рута. В случае модели Каземи, где /См-С/Стр, проницаемость, получаемая по уравнению (4.19), соответствует к аппроксимации /Стр. пл/Стр.

в случае модели Уоррена - Рута, поскольку матрица считается совсем не участвующей в процессе фильтрации в условиях установившегося притока, /Стр.пл = /Стр (уравнение (4.19)). Единственным путем косвенной оценки значения Км является определение параметров, определяющих характер неустановившейся фильтрации (эта методика подробно будет изложена в гл. 7).

4.3.4. Проницаемость трещинных систем упрощенных моделей

Рассмотренная выше оценка проницаемости трещин по лабораторным замерам и данным испытания скважин не связывается с необходимостью знать параметры трещин (их раскрытости, ориентации, распространения и т. д.). Однако по данным о проницаемости, определенной в процессе испытания скважин, можно подобрать эквивалентную геометрическую модель, которая имела бы те же трещинные характеристики и геометрию, используя для этого модели с одной или с многочисленными трещинами. Эта методика позволяет трансформировать результаты, полученные по испытаниям скважин или анализу керна, в результаты для так называемой идеализированной модели трещиноватого пласта-коллектора.

4.3.4.1. Случай единичной трещины

Если единичная трещина подобна трещине / на рис. 4.7, то пустотность ее может быть выражена следующим уравнением:

ф= = А. (4.20)

alh h

Подставив это выражение в уравнение (4.16), получим

Трещинная пустотность и раскрытость трещины связываются с ее проницаемостью, исходя из уравнения (4.21), следующим образом:

6 12 . 22)

b = Y\2hK, = 1/12/,р/Ф,р . (4.23)

4.3.4.2. Случай многочисленных трещин

Модель пласта с многочисленными трещинами, образованная параллельными, одинаковыми по высоте слоями матрицы, которые разделены трещинами, предопределяет параллельное трещинам на-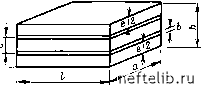

Направление

течения

флюида

Рис. 4.10. Модель пласта с трещинами. Трещины и слои параллельны

правление течения. Такая идеализация позволяет моделировать результаты, получаемые на месторождении, на основе более простой модели фильтрации.

Фильтрация флюида по трещинам (рис. 4.10) может быть описана уравнением

9тр = « X Поперечное сечение потока через трещину X Скорость течения, (4.24)

9тп = nab

тр дя

-i- -= па -

12,0. I

(4.25)

Течение флюида через п трещин может быть выражено по закону Дарси следующим уравнением:

£, тр ДР , Ктр др ?тр = --- = ah

(4.26)

которое не учитывает идеализации условий, так как гидропровод-ность в нем выражена через К-гр и в качестве поперечного сечения потока берется все поперечное сечение пласта S = ah. Из сопоставления уравнений (4.25) и (4.26) следует:

Дтр =

паЬ 12S

паЬ \2ha

Г* тр

= Ф,

62 12

= 4.тр&Дтр,

(4.27) (4.27)

поскольку

А = •"г. тр

па Им

т.тр

Фтр =

nab ah

= Л.тр&