Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 [ 127 ] 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199

	2 1

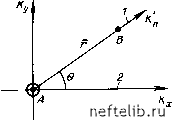Рис. 8.7. Схема, иллюстрирующая интерференцию между двумя добывающими скважинами Л и В в анизотропном пласте.

оси анизотропии: / - большая, 2 - малая

Поскольк у

Рис. 8.8. Схема, иллюстрирующая интерференцию между добывающей а и наблюдательной В скважинами в анизотропном пласте. / - линия, соединяющая скважины, по которой ведутся измерения; 2-большая ось анизотропии

cose

(8.61)

дебит каждой скважины определяется в результате решения уравнения (8.61) совместно с уравнениями (8.54), (8.55), (8.60):

др

(х„Ви In- i

I" скв

vkky =к др

1=4-

(8.62)

(8.63) (8.64)

и-(Кх-Ку) cosn/Kj (YКх + УКу )iYКх

в. Вариант с добываюией и наблюдательной скважинами

Скважина А - добывающая с дебитом Q, наблюдательная скважина В расположена от нее на расстоянии г (рис. 8.8). При стационарном течении распреде-иение давления Р (г) будет определяться уравнением (8.49) с подстановкой в него радиуса скважины (г = гскв) и давления в ней (Р = Рскв).

Для радиуса г в соответствии с уравнением (8.56)

г = Сг {Vk, + v1qi2 vкку,

и зависимость давления от радиуса имеет вид 392

(8.65)

Р(7) = Р,„з + In 1 (8.66)

Подставляя значение дебита Q для установившегося течения из уравнения (8.58) и задавая ij3=l, в сочетании с уравнением (8.67) получаем, что по направлению течения

/ / \2 скв)/(Рдр-Рскв) /О /?0\

= (гдр/гУ е , (8.68)

(8.69)

Далее, угол 6 между большой осью анизотропии и линией, соединяющей скважины, по которой ведутся измерения, получаем из уравнения

cos в/Ко, + sin Q/Ky = F/Кп (8.70)

Очевидно, что если F/K и 0 известны, можно определить направления Кх и Ку.

8.3.3. Оценка анизотропии

8.3.3.1. Большая и малая оси трещинной проницаемости и их ориентации

Как видно из основных уравнений, приведенных выше, относительное расположение добывающей и наблюдательной скважин, дебит и данные о давлении являются основными показателями, необходимыми для определения характеристик анизотропии: Кх, Ку, э и К„ Однако если добывающие и наблюдательные скважины расположены относительно друг друга не по симметричной сетке, то решение проблемы усложняется тем, что количество переменных будет больше, чем количество уравнений (табл. 8.1).

а. Упрощенные варианты

Для преодоления указанных трудностей при решении проблем, связанных с анизотропией, может оказаться весьма полезным исполь-

зование упрощенной геометрии расположения добывающих и наблюдательных скважин. В качестве примеров ниже приводится несколько простых случаев.

Случай 1. Два взаимно ортогональных направления измерений. На рис. 8.9 показано распо.иожение скважин Л, Б и С, из которых А - добывающая, а S и С - наблюдательные скважины, при котором линии АВ и АС образуют два взаимно ортогональных направления аналогично осям Кх и Ку.

Введя проницаемость по направлениям /Си Кс • получим

Кпв1 КпС = Кх1 Ку

и далее

(8.71)

j~ 1в/КпС = Гав/ >\с =

(с-скв)/( др - скв) / Св - скв)/( др - скв) „,

= е / е (о.72)

Отношение Кх/Ку определяется из уравнения (8.72) по данным о расположении скважин (гав, гас) и значений динамического давления Рс и Рв, замеренных в наблюдательных скважинах; Рскв и Рдр, соответственно динамическое давление в скважине А и статическое давление на внешней границе.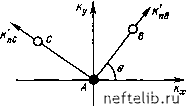

Рис. 8.9. Вариант расположения скважин Л, В и С, когда линии АВ и АС взаимно перпендикулярны

Рис. 8.10. Вариант расположения скважин Л, В, С на одной линии