Главная  Переработка нефти и газа 

Скачать эту книгу

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 [ 186 ] 187 188 189 190 191 192 193 194 195 196 197 198 199

нефтенасыщенности за фронтом вытеснения равно разности водо-насыщенностей л5в = 5в-5в.нач = 0,52-0,27=0,25; эффективная пористость выражается как часть пористости, из которой вытеснена нефть: фэф = фл5в=0,12х0,25 = 0,03.

Решение

I. Теоретические предпосылки

/./. Определения и описание динамики

При рассмотрении вертикального разреза блока (рис. А.1) обычно применяют следующую терминологию: уровень воды - ВНК в тре-щина.х; фронт воды - ВНК в блоках в процессе вытеснения; скорость изменения уровня воды - скорость перемещения ВНК в трещинах {dHsldt); скорость фронта воды - скорость перемещения фронта вытеснения в матрице.

Водяная и нефтяная зоны определяются положением ВНК в трещинах, сумма высот водяной яв и нефтяной ян зон равна высоте блока:

Н,И-=-.Н. (А.1)

Заводненная и незаводненная (нефтенасыщенная) зоны в матрице определяются Z и я-Z.

Нефтеотдача равна отношению ZjHZ, так как предполагается, что в матрице происходит поршневое вытеснение при вертикальном перемещении горизонтальной плоскости раздела вода - нефть. Скорость перемещения уровня воды в трещинах и фронта воды в матрице могут быть представлены соответственно:

v = dHJdt; (А. 2)

и = ФdZ/dt. (А.З)

Силы, которые определяют вытеснение нефти из матрицы - гравитационные и капиллярные. Капиллярные силы возникают в результате особых свойств породы:

= Л,Ат = j (S J а cos б уШт ; (А.4)

Гравитационные силы всегда определяются разностью удельных весов жидкостей, насыщающих матрицу, и жидкостей, заполняющих прилегающие трещины:

с = (яв-2)Ат. (А. 5)

Ряс, Л.1. Схематическое изображение нефтенасыщенного блока матрицы при заводнении: / - нефть в трещинах; 2 - нефть в матрице; 3 - вода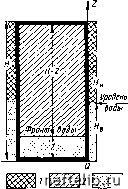

к: j

в особом случае, когда в<2, значение g отрицательно и, следовательно, гравитационные силы препятствуют вытеснению. Если Нв = Н, то

С = (Я-2)Л-г. (А.6)

1.2. Зависимость нефтеотдачи от безразмерного времени

Очень часто для наиболее общего случая блоков не очень большой высоты без существенной погрешности можно допустить, что ВНК в трещинах мгновенно перемещается от нижней грани блока до верхней. Скорость фильтрации «тр = «, связанная со скоростью перемещения фронта воды, задается выражением

а =-+ - д. (А.7)

Лв Лн

которое может быть также записано в виде

и >г1" + (~о) д,, (А.8)

(i„ (1ЛМ)2о+(1-2б)

М = •

Zr, = ZIH.

(А.9)

Зависимость нефтеотдачи от времени получается при подстановке в уравнение (А.8) выражения (А.З):

Л = -i- ФНй {ZIH) = 5 --dZg. (А. 10)

Исходя из дифференциального уравнения (А.10), можно получить следующйе-результаты.

а. Преобладание гравитационных сил

Пренебрегая членом Лк/Я в уравнении (А.10), получим:

J 1-2б

dZn 1 - 2б

1 -.ZdJ

= --1-2е-1п(1-2е)-М1п(1-2б) + Л2д-ь

+ М1п(1-2б),

что окончательно дает

(А. И)

Если уравнение (А.11) записать для безразмерного времени, то получим:

o.rp = (/W-l)Z6-ln(l-Z6).

• гр

(А. 12)

(А. 13) (А. 14)

Эффективная пористость представляет собой часть пористости, соответствующей объему пор матрицы, из которого вытеснена нефть.

б. Преобладание капиллярных сил

Пренебрегая членом (1-2б)Ду, получим

dt =

Z,dZ, +

t = -L [z/2 + MZg - Л12б727: (A. 15)

-L[MZ, + il-M)Z,/2].

Если время записать как безразмерный параметр, получим t,.==MZ, + il-M)Zl/2,

Рк I

(Jti®30(J-hW (J-b (J-b Н

С учетом уравнения {А.4) получим

о.в° ФЛГ crcose у К/Ф К

(А. 17)

(А. 18)

в. проявление капиллярных и гравитационных сил

Ркходя из уравнения (А.10), можно написать дифференциальное уравнение зависимости нефтеотдачи от времени:

dt =

ФН1Ч,

.IldZsM-

M-dZ6

(A. 19)